K-means and Expectation Minimum

本文将简要介绍 K-means 和 Expectation Maximization 方法，可能会以 Gaussian Mixture Models 作为后者的特例进行讨论。

K means

• K means 一般被用于聚类问题，而后者是我们将要介绍的第一种无监督问题。对于数据空间 中给定的若干数据点 ，我们希望按照某种方式将其划分为 种类别，使得这 类数据点互相区分，其中 是预先指定的超参数。K means 算法是求解聚 类问题的经典算法，此处我们为每个类簇指定了中心，并希望使得所有数据点到其类别中心的欧氏距离之和最小。其采取了启发式的思路：

  1. 任意初始化类簇中心。
  2. 对于每一数据点，令其类别为最近类簇中心的类别。
  3. 将类簇中心调整为该类别全体数据点的平均值。
  4. 回到操作二，直到达到了某种终止条件。

  我们可以简单的证明 K means 的收敛性。令 代表每一数据点的分类， 代表 个类簇中心，则优化目标： 可以看作在草做 2 时对 做优化，并在操作 3 时对 做优化，因而 的值在优化过程中必然是单调递减的。显然 ，那么其必然收敛于某一不小于 的值。对收敛速率和解的最优性的更近一步的刻画比较复杂，而且（在本文中）并不重要，此处就不深入了。

Expectation Maximization

• 大多数资料会选择从 K means 引入无监督学习。K means 是一种尤其简单而特别的方式，其（一般）不涉及概率建模，然而在操作上与接下来将要介绍的 EM 方法具备相似之处。¹具体的，在无监督学习中，我们关心的主要问题是如何建模给定数据集的概率分布。而 EM 方法则专门用于处理简单隐变量模型的似然最大化。以下我们需要先介绍一些前置的内容。

概率图模型

• 此处介绍概率图模型的目的主要是为了方便刻画简单隐变量模型。在无监督学习中，我们的终极目的是建模给定数据的分布，然而这一点常常是难以直接实现的。为此，一个合理的切入点是，对于给定数据空间 中的随机变量 ，考虑其与某一隐变量 的关系。这样便可通过 来建模联合分布 ，我们可以对 和 做假设，例如令后者服从高斯分布，以方便处理，这样便得到了 Gaussian Mixture Models 。引入这一隐变量主要是出于两方面的考量：

  1. 在一些问题中，令隐变量 代表“类别”，或是“种类，大小，颜色”一类的语义是自然的。此时我们可以说 是语义空间中的变量，而给定语义时数据的分布假设比较简单，从而方便刻画。
  2. 直接处理数据空间常常难以下手，此时通过引入隐变量 可以简化处理。常见的手段是考察 对于 的条件分布（EM），或是直接刻画隐变量空间到数据空间的概率演化（Diffusion）。

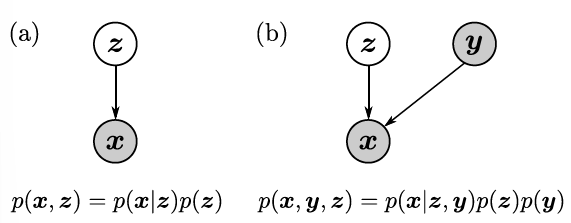
  在具备多随机变量的系统中，我们要考察这些变量之间的条件关系。对于随机变量 ，假定存在有向无环图 ，记 代表节点 在 中的全体前驱，则若： 称 刻画了一个概率图模型。概率图模型中的某些点在数据集中是不可见的，这些点便被称作隐变量。常见的模型，例如 EM 和 conditional VAE 的概率图模型形如：

  

  其中浅色点代表隐变量。

最大似然估计与贝叶斯推断

• 本节的主要目的是澄清一些机器学习中和统计推断相关的术语。绝大部分资料中不会关注这一部分，然而对于不熟悉统计推断的读者来说这些术语很可能造成理解上的障碍。以下我们将从频率学派和贝叶斯学派两方的看法，分别介绍最大似然估计和贝叶斯推断。此处的核心是贝叶斯公式：

  我们给贝叶斯的各项如上命名，翻译为后验 posterior ，似然 likelihood ，证据 evidence 与先验 prior 。首先我们需要说明各项的名字并不因为公式的方向而改变，而是由语境决定，即统计推断中总是有一定的推断方向，而各项的命名是遵从这一方向的。

  统计推断在方法论上分为两派，其中频率学派更关注随机试验，其认为只有在大量随机试验下才可以讨论概率，而概率应是一无法直接观测的确定值，我们希望通过一定的方法估计这一定值，并给出置信度。在这一视角下，对参数 谈先验是没有意义的。我们认为参数存在某一真实值，而我们希望通过最大化似然的方式来估计参数，这便是最大似然估计。

  而贝叶斯学派认为概率来源于主观信念，其表达了主观上认为某事发生的概率。既然如此，对于任意的事件都可以存在先验，而我们可以通过观测，利用似然和证据来修正先验，得到后验，即利用已有的事实更新主观信念。这一计算后验的思想便被称作贝叶斯推断。

证据下界的推导

• 对于给定的数据集 ，以及模型建模得到的概率分布 ，我们希望优化数据点 服从 的似然，即： 另一方面，在贝叶斯推断的看法中， 。在简单隐变量模型中，建模 的方式是对 做边缘化（以下考虑单个数据点）： 此时 被视作关于 的贝叶斯公式中的证据，注意先验 是固定的。我们不希望直接处理积分，因此先考虑构造琴生不等式把对数放入内部。对于任意的分布 ，应有： 上式给出了关于 的对数似然的下界。我们希望通过选取恰当的 使其给出尽量紧的界，由于 作为分布可以被视作函数，因此这一函数空间上的优化被称作变分下界（Variance Lower Bound）。另一方面，由于 是关于 的证据，上式也被称作证据下界（Evidence Lower Bound）。为了给出尽量紧的估计，考虑对于 优化，一个看法是在值： 固定时，琴生不等式取等，这意味着： 另一方面，一个更直观的方式是，考虑： 因此： 这同样说明在 时，下界是紧致的。另一方面，注意到在固定 时，优化证据下界等价于优化 ，这是一个很好的结果，因为 在假设中往往是已知的，若 具备好的解析形式（例如在 GMM 中），便可得到该期望的解析解。

  以上的讨[论给出了直接的优化关于 的对数似然的思路，这便是 EM 方法。具体叙述如下：

  1. 随机初始化参数 。
  2. 由证据下界的形式，令 ，此时可以看作固定 时优化 ，该步称 Expectation Step 。
  3. 对 做 MLE ，此时可以看作固定 时优化 ，该步称 Maximization Step 。
  4. 回到第二步，直到达到某种终止条件。

  其中第二步称 Expectation Step 的原因应当是其通过固定变分分布 ，构造了第三步的优化目标，即关于 的后验对数期望。以上，可以看出 EM 的重点是通过引入变分分布 推导得到证据下界，并交替的优化 和 以避免直接处理积分。

  类似于 K means ，容易看出 EM 的主过程等价于交替的优化证据下界，从而其总是单增的。更进一步，记第 轮 EM 时的参数为 ，变分分布为 ，证据下界为 ，容易看出： 这说明对数似然也是单增的。我们期待对于合理的概率建模，对数似然总是有界的，因此 EM 是收敛的。

  此外，若 不存在好的解析形式（例如 VAE ），我们便需要用其它手段（非 EM ）来优化 ，使得 尽量与 接近。因为“计算后验”这一操作也称贝叶斯推断，以上使用变分分布近似后验的方法便被称作变分推断。

---

1. 实际上 K means 也许视作 EM 的特例，不过我认为比较牵强，且没有必要。↩︎