本文介绍了 Support Vector Machines ，使用 Lagrange Duality 推导了 Hard SVM 的对偶形式，并使用表示定理导出了 Soft SVM 的一般形式，讨论了选取复杂核函数时对 Soft SVM 的解读。

Support Vector Machines

• 支持向量机是一类广泛使用的模型。其中心思想与先前基于概率建模并使用 MLE 优化的模型不同¹，应只能使用 ERM 优化。具体的，考虑一个二分类问题。假定数据空间 ，数据集为 ，其中 。注意此处标注集合与先前的 不同，这是因为后者更适合概率建模，而取 作为标注则更方便 SVM 的分类。

• 现在我们希望找到 中的超平面 使其最好的区分了两类数据点。假设存在超平面 完全区分两类数据，则出于健壮性的考虑，我们希望所有数据点到 的最小距离尽量大。对于 ，容易看出 到 的欧式距离为：

  一个简要的说明：对于 ，取 使得 。注意到 平行于 ，因此：

  则写出该问题的优化形式： 该模型被称作 Hard SVM ，即我们强制要求平面 完全区分两类数据点。以上形式比较复杂，注意到对于 乘任意非零常数不改变几何平面，因此令 ，得到： 显然取得最优解时， 必然满足，从而： 这便是 Hard SVM 的标准形式。对于使得约束取等的点，我们将其称作 support vector 。显然，在最优解中两类数据点中必然各自存在 support vector 。观察以上形式，这是一个凸二次优化问题，可以直接使用数值求解器，然而更好的选择是考虑其对偶问题。

Lagrange Dual

• 参照先前对于 Lagrange Duality 的讨论²，定义 Lagrangian ： 则 的对偶问题写作： 由 Slater's Condition ，带有仿射不等式约束的凸优化问题显然具备强对偶性，这就是说 和 的最优解是相同的。熟知任意优化问题的强对偶点必然满足 KKT 条件，即：

  1. 驻点性。 。
  2. 可行性。 。
  3. 互补松弛性。 。

  选择条件 1, 3 代入 ，得到： 化简得到： 这是一个很好的形式。一方面来说该形式只包含数据点的内积，因而可以方便的套用 Kernel Trick ³；另一方面，该形式具备较为高效的优化算法 SMO（Sequential Minimum Optimization）。

• 值得一提的是，观察 SVM 的标准形式 ，其中包含了项 ，恰为系数 的 范数，可以发挥类似正则项⁴的作用。我们知道通过 Kernel Trick 可以将 SVM 的数据点投影到极高维的空间中，而数据点实际上很难在高维中充分的分布。即使如此，不加正则化的 SVM with Kernel Trick 也不会容易的过拟合，原因之一便是其自带某种正则化的功效。

Soft SVM with RKHS

• Hard SVM 的假设实际上是非常理想的状况，实践中的数据集往往不是线性可分的，这就是说问题 的可行域为空。为此，考虑修改目标函数，不再硬性要求平面 完全区分数据。具体的，我们希望为分类错误的点带上额外的惩罚，从而写出如下的 ERM 形式： 其中 称惩罚系数，第二项应有不同的设计方式，此处选择的是 hinge loss 。改写得到： 到这里便可直接使用 Lagrange Duality 等方法优化，但我们不满于此。定义： 即 是全体 的线性函数的函数空间。此处丢弃偏置项 是为了与先前的表示定理统一而做的妥协。改写得到： 其中 上的内积就定义为 维欧氏空间的内积。定义再生核： 验证再现性： 从而 是具备再生核 的 RKHS 。由表示定理，问题 的最优解可以写作： 令 代表矩阵 ，称 gram matrix ， 代表 的第 个列向量，得到形式： 这便是选取 中线性函数作为分类平面的 Soft SVM 的最终形式，使用 Lagrange Duality 应该也能得到相同的结果。

SVM with different Kernels

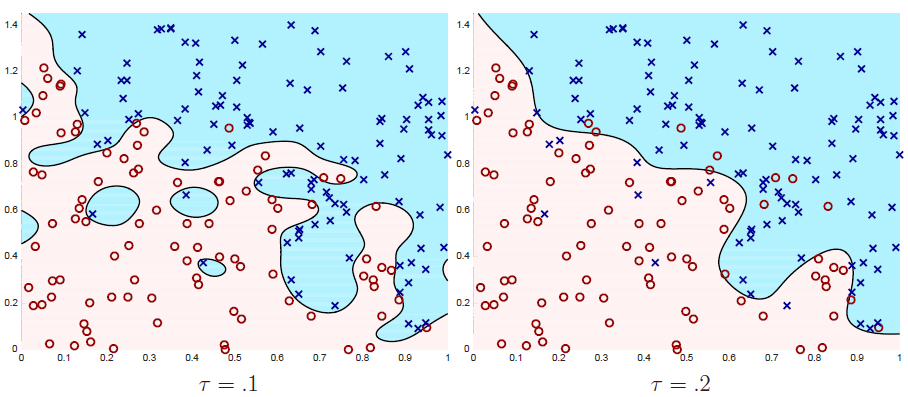
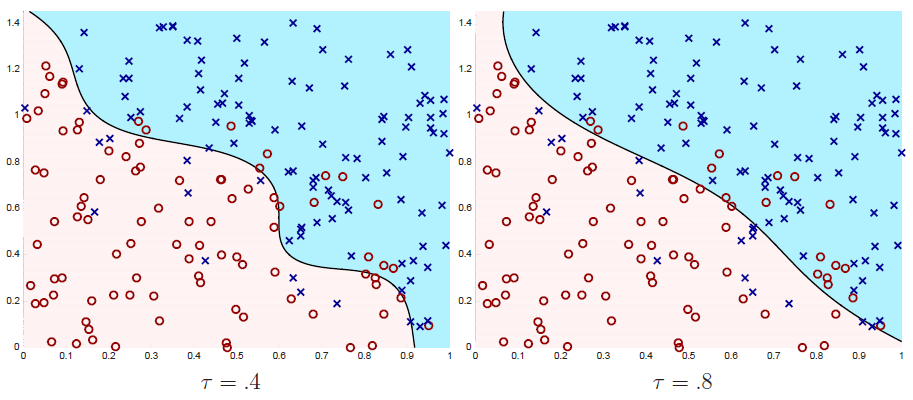
• 按照表示定理，通过替换不同的核函数 ，我们可以在不同的函数空间 中做优化。因此我们好奇在给定更复杂的核 时有什么意义。一个简单的看法是，我们将再生核 作为特征函数，将所有数据点映射到高维欧氏空间中，再做线性函数的 Soft SVM 。另一基于表示定理的观点则是通过更换核 ，也就更换了做 ERM 时选择的函数空间，此时 hinge loss 仍然以某种方式度量了数据点的分类正确性。

• 一个常见的例子是选择高斯核： 其中 称带宽（bandwidth），控制了内积的敏感性。固定 ，通过选择不同的 并按照式 优化，可以得到不同的分类边界：

  

  

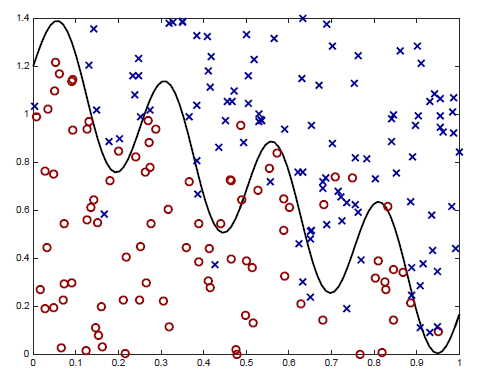
  以示对比，下图展示了真实的分类边界（我们期望在提供的数据点趋于无穷时模型可以收敛到这一情况）：

  

---

1. 先前介绍的模型总是可以做概率建模的。↩︎

2. 以下所述均建立在前文《最优化方法/拉格朗日对偶性》的理论框架下。↩︎

3. 该形式可能无法直接使用表示定理解读，但仍可以视作在高维空间中做 Hard SVM 。↩︎

4. 虽然我们还没有正式介绍正则化。↩︎