Generative Learning Algorithms

本文介绍了与先前的判别式算法不同的生成式算法，特别是 Gaussian Discriminant Analysis 和 Naive Bayes 。

Generative Learning

• 我们先前介绍过生成式模型，此处的生成式学习与其建模的概率分布是相同的。具体的，仍考虑二分类问题，对于先前的算法（如逻辑回归），本质上我们希望直接学习分布 ，并将最终分类规定为： 而对于生成式模型，我们将不再直接学习 ，而改为学习 。这样，按照贝叶斯公式： 我们同样可以得到 。这样做的好处是有时直接建模 是困难的，而通过贝叶斯公式我们可以绕过这一点。因为我们学习了 ，理论上我们可以通过从该分布中取样来生成，这套框架就被称作生成式学习。

Gaussian Discriminant Analysis

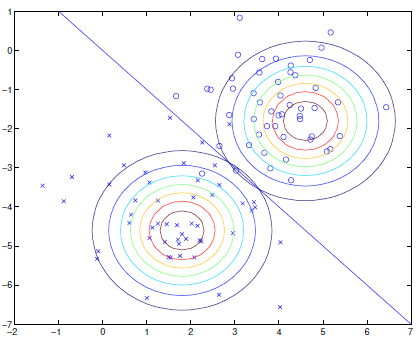
• GDA 是典型的生成式学习算法。具体的，此处的假设是 服从高斯分布。具备均值 与协方差矩阵 的高斯分布的概率密度函数为： 我们先承认这一点，因为我其实不熟悉协方差那一套。对于标准的二分类 GDA 模型，其假设为： 注意此处两个条件分布的协方差矩阵是相同的，这其实不是一个必须的假设，也有模型选择对两者做不同的参数化。这样做的好处是参数量更少，而且分类边界是超平面。考虑如何训练上述模型，我们仍然采用 MLE ，不同之处在于此处的优化目标是： 即联合分布，而此前的判别式模型的优化目标则是条件分布。这一方面是因为后者不对数据分布建模，另一方面也是因为其只需要做分类任务，而生成式模型学习到的东西则更为完整。那么，按照上式推导，容易得到在最小化联合分布的似然时有： 一个二分类 GDA 的分类边界示意图如下所示：

  

  注意当高斯分布的协方差 同参数化时，分类边界总是线性的，其由 给出。

GDA 与逻辑回归

• 在 GDA 的最终分类时，我们关注的是 ，若将其视作关于 的函数，则其可以被写成： 其中 仅与 相关，而这服从逻辑回归的形式。反过来，逻辑回归的假设就不意味着数据分布是高斯的，例如对于服从泊松分布的 ，我们同样可以导出逻辑回归。

  以上的讨论说明 GDA 是比逻辑回归更强的假设，即 GDA 总是逻辑回归的特例，但这并不意味着逻辑回归总是强于 GDA 。一方面来说 GDA 的假设更多，因此在数据更少时可以较为充分的建模，而逻辑回归一般需要更多的数据来充分的学习。而在 GDA 的假设失效，即数据不服从高斯分布时，逻辑回归几乎必然表现得更好。

Naive Bayes

• 先前介绍的 GDA 用于建模连续数据分布，而若数据分布是离散的，此时可以采取其它方式处理，例如 Naive Bayes 。Naive Bayes 同样是生成式算法，其不对数据分布做假设，而要求了分布各维的独立性。具体的，考虑垃圾邮件分类，我们希望预测给定邮件是否是垃圾。对于任意的邮件信息，我们希望将其建模维为特征向量，具体的方式是对于数据集以 token 的形式构建字典。假定字典的大小为 ，则任意邮件的特征为 中的向量，每一维落在 中，代该表 token 有无出现。

  现在问题转化为对于 中的 向量 分类，预测其二分类标签 。按照生成式学习的框架，我们希望学习 。由于数据空间 是离散的，我们希望直接建模 的分布，然而 太大了。为此，假设 的每一维在给定 时是独立的¹，即： 这样便只需对 个服从伯努利分布的随机变量建模。将概率参数化，使得： 按照如上所述的 MLE 进行优化，记数据集为 ，则： 这就是 Naive Bayes 最终的结果。

Laplace Smoothing

• 以上最基本的 Naive Bayes 会遇到实践上的问题。若字典中存在词，比方说，Su30sm，然而 Su30sm 并没有在数据集中出现过，那么其频率会是 ，这会导致所有与其相关的参数取 。那么对于包含 Su30sm 的特征 ，按照贝叶斯公式计算得到 ，这是没有意义的。为此有一个简单的修正方式，即为所有 token 的出现次数带上额外的一次。这样参数修改为： 特别的， 用不用 Laplace Smoothing 一般不重要，因为其本身的值受每分类加一的影响不大。

• Laplace Smoothing 不是单纯经验的解决方案，这是由 Laplace 提出的解决此种“频率为 0 ，然而客观概率不应为 0 “问题的办法。其理论上的基础大概是为所有类别设定先验概率，然后根据频率计算其后验。此处不打算进一步深入其推理。

Event Models for Naive Bayes

• 此处的 Event Models 值的是 Naive Bayes 建立特征向量，进而建模其概率的方法。不同于考察每一 token 的出现概率，我们可以将邮件视作若干 token 构成的字符串。假定邮件的每一个 token 在字典中的选择在给定标签 时是独立的，假定邮件 的 token 个数为 ，第 个 token 为 ，则联合概率可以写作： 这样我们建模了 个 种取值的随机变量，与原先 个伯努利变量区分。仍然使用 MLE 对其优化，得到： 类似的也可以添加 Laplace Smoothing 。特别的，这种建模方式得到的 Naive Bayes 似乎会比先前的建模方式更好些。

• 对于连续的问题，我们往往可以通过某种方式离散化其值域从而应用 Naive Bayes ，一种常见的方式是将值域分段。值得一提的是 Naive Bayes 简单且无需迭代，性能也常常不差²，因此将其作为最初的选择或许是较为合理的。

---

1. 这是妥协。↩︎

2. 这话是 2018 年的时候说的，我估计 Naive Bayes 和如今的语言模型肯定没得比。但 Naive Bayes 实在是一种很简单的方法，以至于非常适合在终端上部署。↩︎