Linear Regression

本文介绍了一些基本的术语，以及线性回归与 Locally Weighted Linear Regression 。

Supervised Learning

• 机器学习中有很多术语，而某些资料却不会介绍它们的意思，造成不必要的麻烦，因此此处我们会尽量解释所有的术语。我们知道机器学习本质上是数据科学，即我们期待在不显式编程的前提下，让计算机从庞大的数据集中学到一些不平凡的性质。我们说一个机器学习算法是监督学习，若数据集带有（人工的）标注，例如分类；反之，无监督学习就是不要求数据标注的机器学习算法，例如现今的生成模型。

  特别的，我们总是偏好无监督学习，因为其不需要人工标注，从而可以方便的进行大规模的训练。但最初的机器学习算法大部分都是监督学习。在此基础上还有更细致的分类，例如弱监督、自监督等，这里就不深入了。

Linear Regression

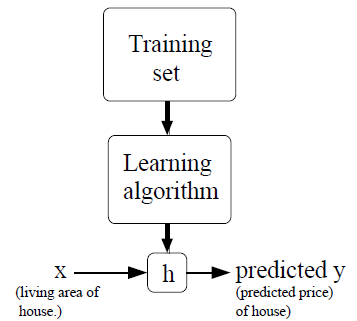
• 我们从最简单的监督学习——线性回归讲起。假设我们有数据空间 中的数据点 ，每一个数据点带有标注的标签 ，其中 称标签空间。给定任意的 ，我们希望预测 的标签 。“古典”的机器学习框架如下所示：

  

  即我们希望通过某种学习算法从数据集中学习得到一个映射 ，使其预测每一个数据的标签，我们将 称作假设（hypothesis）。¹若标签空间 是离散的，我们就说这是一个分类任务；而若 是连续的，我们就说这是一个回归任务。

• 现在考虑最简单的情形，假设 ，并且 是仿射的。那么对于参数 ， 必然服从： 注意此处 的角标是为了凸显其关于 参数化。方便起见，我们为 添加一维 ，并将 作为 的第零维，从而将 写成 。现在我们希望找到最适合手上数据集的参数 ，为此我们定义经验风险函数²： 我们希望通过最小化 来找到最合适的 ，上述方法便被称作经验风险最小化（Empirical Risk Minimize）。

• 现在我们考虑如何对 最小化。为此，有两种方法，其一是梯度下降，考虑： 按照梯度下降³进行优化即可。另一方面，容易看出 是可微的凸函数，因此容易得到其解析的最优解，这里暂且不赘述了。⁴

线性回归的概率解释

• 先前我们使用的办法是 ERM ，即没有解释为什么选择了 范数作为度量。现在我们给出一个基于最大似然估计（Maximum Likelihood Estimation）的解释。机器学习中的似然这一概念主要有两类意思：

  1. 对于连续随机变量 ，我们说 为 的似然。
  2. 对于参数 ，其刻画了一个假设 ，我们说 为参数 的似然。为了表明 的影响，我们常把概率写成 。

  那么最大似然估计的目标就是最大化 。特别的，此处的分布很有可能是连续的，此时使用概率密度替代即可。

• 对于给定的 ，假定假设 是（一定程度上）正确的，即对于任意的数据点 ，其预测值是 ，标注为 ，我们假定预测是正确的，而标注受到外界因素（例如人工误差）影响，从而具备误差 。由中心极限定理，我们期待 服从高斯分布，即 ，其中 为一常数。现在我们希望找到某一 ，使其最大化以上所述成立的似然，即：⁵ 由于积是难以处理的，我们常常会处理对数似然： 现在将高斯分布代入，容易得到： 而优化以上目标和 ERM 并没有区别。这样，我们就从一个较为自然的角度说明了为什么 ERM 中选择了 范数。

Locally Weighted Linear Regression

• 该算法简记为 LWR 。我不知道 LWR 有什么深刻的数学，但其引入了一些新概念，所以简要的介绍一下。对于原先的线性回归，其从数据集中学习到了参数 ，然后就不再需要数据集了，因此我们说这类算法是参数化的（parametric）。而 LWR 则是非参数化的。具体的，要预测数据点 处的标签，我们希望找到参数 使其最小化： 并令 ，其中 为事先决定的参数，称带宽。我们期待以上局部加权的回归方式可以更精细的反映 处的性质。而该算法的参数总是原地计算的，因此我们需要保存全体数据集，这被称作非参数化（non-parametric）的学习方法。

  特别的， 也有别的选法，而且 LWR 也有些别的性质，此处就不深入了。

---

1. 这似乎是某种历史原因，不过我认为大致的意思应该是我们假设数据与标签的关系服从这一映射吧。请注意本文中的“假设”因此有两重意思，对应英文语境下的“assume”和“hypothesis”，请根据语境区分。↩︎

2. 也可以叫损失函数或是花费函数。↩︎

3. 参照深度学习。↩︎

4. 具体怎么操作是最优化方法的事，我们已经讨论过如何处理向量值函数微分。↩︎

5. 以下我们对于概率的写法与严格的概率论会有区别，所以请结合语境。↩︎