拉格朗日对偶性

从 Lagrange Condition 到 KKT Condition 再到 Lagrange Duality 基本是层层深入，我们会渐渐的介绍对优化问题更深入的刻画。

Lagrange Duality

• 回忆在先前介绍 KKT 时，我们将 Lagrangian 定义为： 其定义域为 ，是一个开集， 。现在我们考虑将原优化问题： 写成关于 Lagrangian 的 minimax 优化的形式。对于 ，其中 为可行域，注意到 ，这说明： 而对于 ，显然 不存在，认为其取 。那么对于 就有： 注意上式对于任意优化问题都成立，并且不要求 。这样，我们就把原优化问题写成了对于 Lagrangian 的 minimax 优化问题，并且不需要考虑可行域。我们将以上形式称作原问题的 saddle point formulation ，这是一个很优美的形式，以下关于对偶的讨论都是对于 saddle point formulation 谈的。

  我们好奇在交换 minimax 的顺序时类似的关系是否仍然成立，即是否有： 这便被称作原问题的对偶问题。更确切的，定义拉格朗日对偶函数： 则对偶问题写作：

  • Remark. 我们所指的的 Lagrange Duality 是 到 的转化。特别的， 的对偶不一定是原问题。

对偶问题的性质

• 对偶问题有一个很好的性质，就是其一定是凹的。按定义： 注意到 是关于 的仿射函数，而对一族仿射函数做逐点 得到的结果显然是凹的。这就是说通过 Lagrange Duality 得到的 dual problem 一定是凸优化问题。

Weak Duality

• 既然按照以上的形式定义了 lagrange duality ，一个自然的问题是原始最优解 等于对偶最优解 是否成立。一个简单的看法是，显然， 总是成立的，这被称作 Weak Duality 。更广泛的，我们有：

  • 【定理 1. Minimax Inequality】对于集合 和函数 ，有： 简单的说，内部的运算决定了 Minimax Inequality 的方向。

  证明：考虑：

  那么由以上定理，Weak Duality 显然成立。

• 现在我们希望关注更强的性质，即 Strong Duality 是否成立。这是一个很难的问题，以下我们将逐步回答。

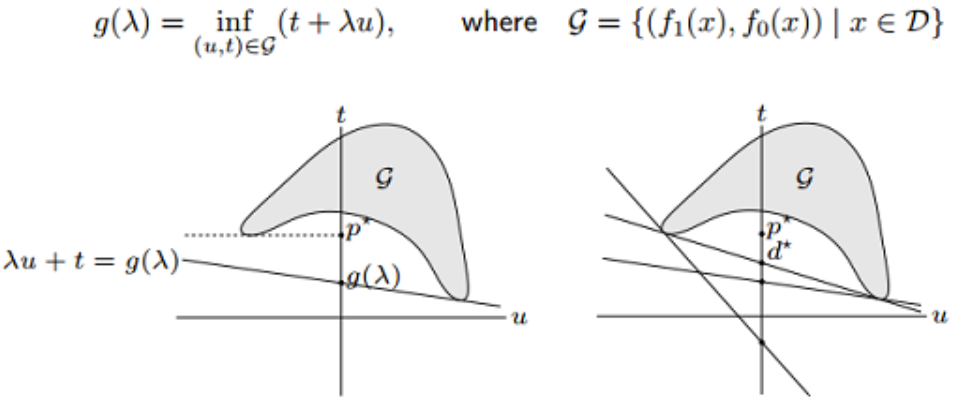
Geometric Interpretation of Duality

• 以上定义的对偶问题看起来比较抽象，所以现在我们考虑如何从几何直观上建模 Lagrange Duality 。我们先考虑定义域 上全体函数点的集合。即对于优化问题： 定义：

  固定 ，则对于 ，考虑： 这就是说选定 时，随之确定了 中的点，按照 Lagrangian 的形式得到此处的取值 。将其变形为： 看作 的仿射函数，那么 dual function ： 便视作固定梯度 （即超平面的方向）时取全体经过 中点的超平面的最小截距¹。而对偶问题： 就视作取遍全体方向时最大的截距。举例如下图所示：

  

  注意到 对应的超平面也可以说是 的支持超平面。

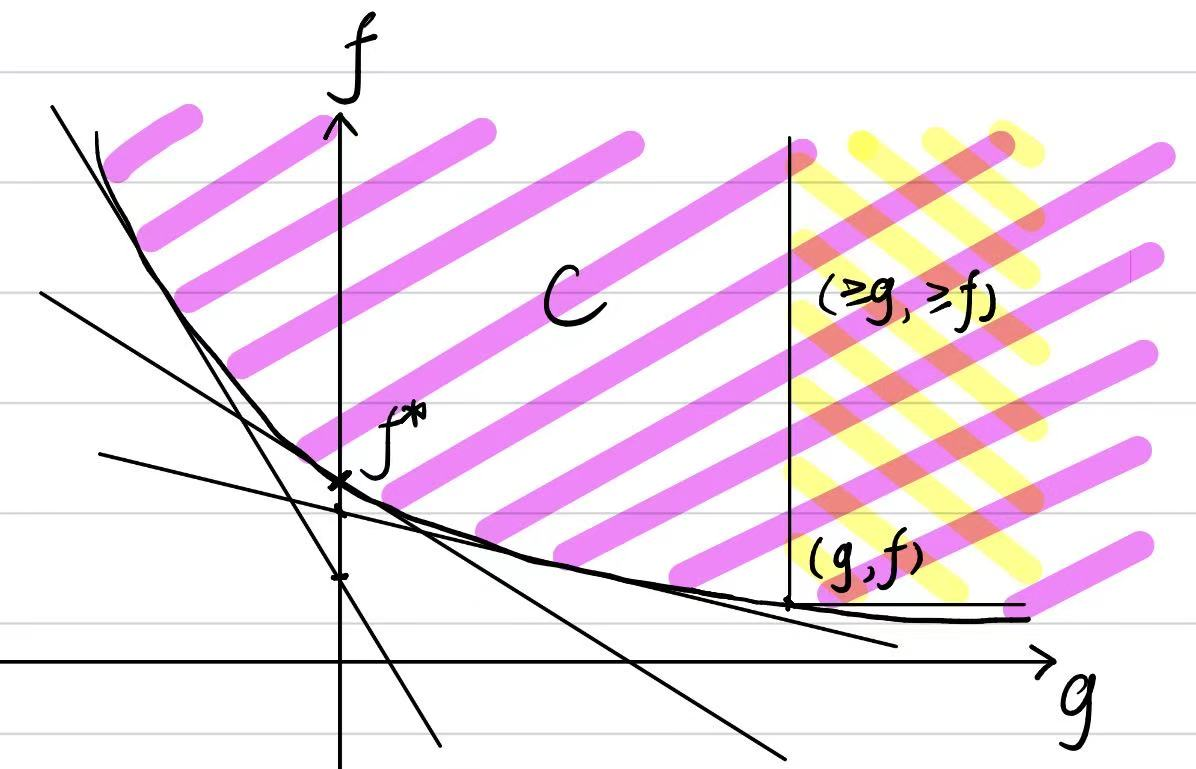
Strong Duality

• 在以上的几何解释中，对偶问题的目标转化为用所有的支持超平面去切集合 ，以截距逼近 在纵轴上的最低点 。如果 是凸的，我们期待总是能找到一个超平面恰好切到 。遗憾的是 往往不凸，为此，我们要做一些修改。考虑集合： 显然 与 的作用是一致的，因为总是有： 成立。而在用 替换 的好处在于，若原问题是凸优化，则 是凸集，而且 的所有支持超平面的梯度一定满足 ，²如下图所示：

  

Slater's Condition for Convex Optimization

• 综上所述，对于凸优化问题，我们几乎想要断言其必然满足 Strong Duality ，然而问题是仍存在情况无法找到切 于 处的支持超平面。这主要是因为支持超平面是关于梯度参数化的，从而无法表达梯度不存在（即平行于纵轴）的情况。一个典型的例子是： 其 为：

  

  为了保证切 的支持超平面存在，我们要求横轴左侧区域不能为空，形式化的：

  • 【定理 2. Slater's Condition】对于服从形式 的凸优化问题，若存在 使得 且 ，则 Strong Duality 成立。

    其中 代表相对内点（relative interior）。

  证明：[Admitted]³

  • Remark. 该定理直观上说的事情是，我们要在纵轴上找到一个点，使其对于所有不等约束在横轴左侧不为空。不用关注等式约束是因为凸优化的等式约束总是仿射的，因而是平凡的。

KKT conditon and Duality

• 以上的 Slater's Condition 对于凸优化的强对偶性给出了较弱的要求，即保证了强对偶性的存在，而没有给出具体的对偶最优解。我们知道先前介绍的 KKT 条件，其服从：

  1. 驻点性。 。
  2. 可行性。 。
  3. 互补松弛性。 。

  是凸优化的最优点的充分条件，我们好奇其是否保证了强对偶性。具体的，有：

  • 【定理 3. Sufficiency of KKT for Convex Duality】对于服从形式 的凸优化问题，若存在满足 KKT 条件的解 与 Lagrange multiplier ，则强对偶性成立，且：

  证明：熟知 KKT 是凸优化的充分条件，从而容易看出 。按定义： 从而强对偶性满足。

• 事实上我们可以进一步加强以上定理，即说明 KKT 是凸优化的强对偶性存在的充分必要条件。考虑：

  • 【定理 4. Necessity of KKT for Duality】对于服从形式 的一般优化问题，若强对偶性成立，即存在 和 使得 ，则 满足 KKT 条件。

  证明：按定义： 因此： 现在逐条考察 KKT 条件：

  1. 驻点性：由于 且 是开集，必然有 。
  2. 互补松弛性：由于 ， ，容易得到 。
  3. 可行性：自然成立。

  这就是说对于任意优化问题，满足强对偶性的点必然也满足 KKT 条件。

• 综上所述，我们概括对于凸优化问题，强对偶性存在当且仅当 KKT 条件满足。更确切的说，某一点 满足强对偶性当且仅当其满足 KKT 条件。比较 KKT 条件和 Slater's Condition ，我们发现前者似乎更强，但这并不意味着后者没用。主要原因在于 KKT 条件更加复杂，且必须要找到合法点 才能断言强对偶性存在，且 恰满足强对偶性；而 Slater's Condition 则更加简单，如果只需要确保强对偶性存在，以转而优化对偶问题，其应为更好的选择。

---

1. 如果各位熟悉斜率优化的话可能会对该形式有印象。↩︎

2. 这两点是容易验证的。↩︎

3. Slater's Condition 的证明疑似有点又臭又长，我估计大家不会想看的。↩︎