等式约束优化问题的拉格朗日条件

我们将在这里尽量详细的介绍等式约束优化问题的 Lagrange condition ，我会尽量以符合直观，并且严谨的方式来写。

特别的，阅读本文应该需要一定的凸优化基础。方便起见，文中的向量就不加粗了。

带有等式约束的凸优化问题

• 为了提供直观，我们从带有等式约束的凸优化（Convex equality constrained problems，CEC）讲起¹。考虑优化问题： 其中 ，我们要求 是凸函数，并且可行域不为空，这就是说其可行域是凸集。那么，上例是带有 个线性等式约束的 维空间中的凸优化问题。其可行域为： 给定任意 ，熟知： 其中 为 的行向量的零空间。其恰为 中点 处所有”可行的方向”。我们推广可行域中某一点处的“可行方向”的概念，就得到了如下定义的切空间。对于 ，称 为 处的切向量，若存在一可微的函数 （称为路径），使得 ，且 。而 处的全体切向量就构成了该处的切空间，记作 。

  切空间的直观是，对于可微的 ，我们在 处对 做线性近似，这样切空间就基本描述了该处 所有可行的方向。在上例中，总是有 。

  进一步定义 处的法空间 为切空间的正交补，即 ，使得： 容易看出上例中 每一点的法空间恰为 的（行向量）的张成，记作 。²特别的，切空间与法空间总是线性空间。

CEC 的拉格朗日条件

• 现在我们考察上例的最优解应满足何种条件。我们有：

  • 【引理 1】对于可微的目标函数 与集合 ，使得 上每一点的切空间均存在，则对于 在 上的最优解 ，有：

  这是一个简单的结论。假设存在任意一个 不满足条件，则其正反方向的路径必然有一条在 处导数为负，产生矛盾。

• 在以上观察的基础上，我们可以给出 CEC 的拉格朗日条件：

  • 【定理 1】 是 CEC 的最优解，当且仅当存在 使得：

  先证必要性。由【引理 1】，我们知道 ，这就是说 落在 中，其自然可以被行向量线性表出。再证充分性。考虑凸性的一阶条件，应有： 拉格朗日条件有一个更紧凑的写法，也就是所谓的拉格朗日函数： 这样【定理 1】的条件可以直接写作 。

一般等式约束问题

• 现在我们考虑带有等式约束的一般优化问题（General equality constrained problems，GEC），即： 其中 ， 不一定凸，我们要求 可微，并仍记可行域为 。现在我们希望推广 CEC 中的讨论到 GEC 中来。为此，仿照先前的方式定义 在 处的切空间为 ³。对于任意 ，其对应路径 ，使得 且 。我们有： 这说明： 这就是说 ，即 。按照先前的经验，我们期待 成立，然而这却不一定总是对的。具体的，对于 ，我们称其为正则点（regular point）当且仅当 的 个分量线性独立；否则称其为临界点（critical point）。这里的直观是，在正则点处， 的局部信息可以被一阶导数完全描述。

  

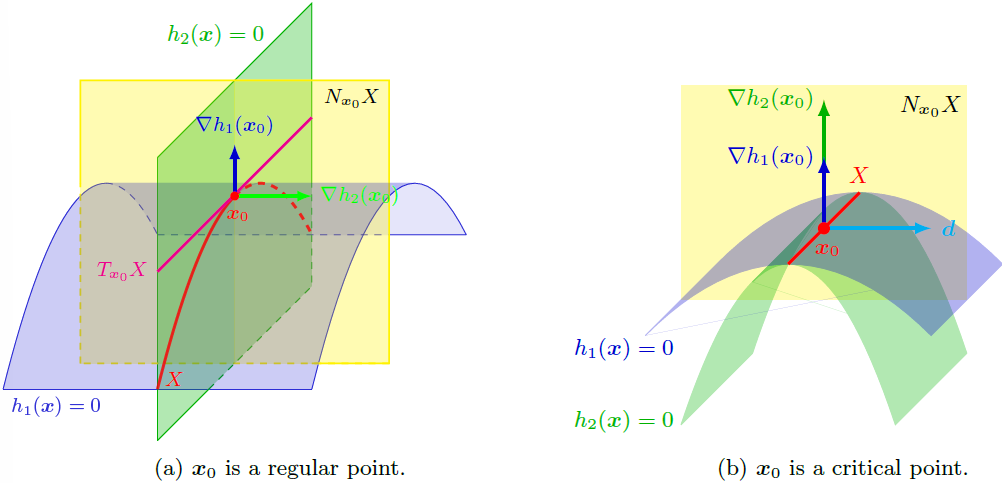
  上图是正则点和临界点的例子。在正则点处，约束的梯度完全刻画了法空间，使其张成的零空间恰为切空间；而在临界点处，约束的梯度却不一定可以完全刻画法空间。

正则点的性质

• 现在我们将要严格证明正则点的良好性质。我们的工具是隐函数定理：

  • 【定理 2】对于连续可微的 ，记 中的坐标为 ，其中 。给定 使得 ，若 可逆，则存在 的邻域 ， 的邻域 ，以及唯一的连续可微函数 ，使得：

  [Admitted]⁴

  这样我们就可以证明以下引理：

  • 【引理 2】若 是 GEC 的正则点，则 ，存在一条路径 使得 ， 且 。

  令 ， ，注意到： 并且： 由于 列满秩，显然 可逆，从而由【定理 2】，存在 使得在 充分小时有 ，且： 那么令 ，就有 ，且 ，故原命题得证。

  通过【引理 2】，立刻可以得到：

  • 【定理 3】对于 的正则点 ， 。

  特别的，临界点不一定不满足 ，例如我们先前提到的 CEC 。这里的直观是，因为存在 个约束，所以变量自由度至少为 。在正则点处，因为可以用 个变量表出其余 个变量，所以变量自由度便只能为 了，这占满了所有的 维，造成了正交补。而在临界点处，虽然约束的梯度不一定线性无关，但是切空间可以更大，也可能造成正交补。

GEC 的拉格朗日条件

• 通过【引理 1】与【定理 3】，我们可以得到以下的定理：

  • 【定理 4】对于 GEC 的极值正则点，必然存在拉格朗日乘子 ，使得： 类似的，定义 Lagrangian ，则以上条件归结为 。

  以上，Lagrangian 的用处基本是将带约束的优化问题转为无约束的极值求解问题。特别的，【定理 4】给出的是正则点处极值点的必要条件，另外临界点处的情况也是需要额外验证的。

---

1. 凸优化的等式约束必须是仿射的，不等式约束必须是凸的，这是为了保证单个约束的可行域也是凸集。↩︎

2. 应该很容易看出任意矩阵 的零空间和张成互为正交补吧。↩︎

3. 如若不特别说明，均要求切空间存在。↩︎

4. 找个时间详细写这个。↩︎