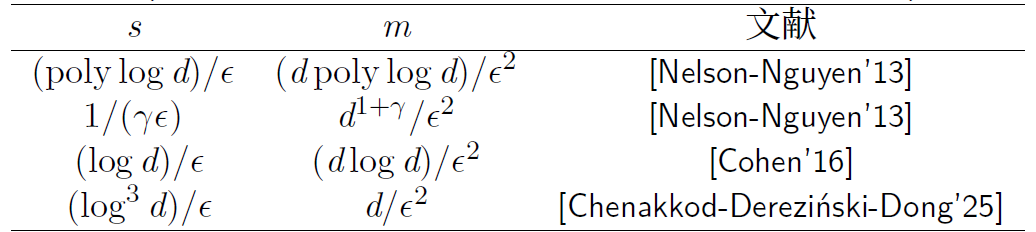随机数值线性代数

随机数值线性代数看起来不是一个很经典的方向，但是里面的理论还是相当有趣且深刻的，我们将会在这里介绍一些基本的内容。

特别的，由于这是一个新兴的方向，lecture 里面的结果都是离现在较近的，且带有一定的综述性质。另外出于时间上的问题，lecture 跳过了部分引理的证明。

最小二乘问题

• 随机数值线性代数的引入是为了解决这样一类问题：实践中有对大规模线性代数快速求数值解的需求，而基本的算法，例如矩阵求逆，的复杂度太高而无法接受。对于形如稀疏矩阵的情况而言，我们期待有时间上效率更好的方法，为此我们可以接受一定的误差，这就是随机数值线性代数。

  现在我们从一个简单的问题引入，即最小二乘。对于列满秩的 与 ，其中 ，求解： 以下我们默认范数指代 范数。

• 容易推知最小二乘问题具备显式解 ，使用基本的方法求解该式的复杂度为 ，然而读取输入复杂度为 或 ，其中 为非零系数个数。我们期待求解复杂度可以逼近输入复杂度这一下界。

子空间嵌入

• 具体的，注意到 为 的一低维子空间，我们希望将其嵌入一低维空间中以缩减问题规模，这就是子空间嵌入。给定列满秩的 ，称 为 的带有畸变 的子空间嵌入，当且仅当： 这就将 的列空间嵌入了 。对于最小二乘问题，如果我们取得了 的子空间嵌入 ，我们就有 在 之间，从而我们期待只需求解问题： 就可以逼近原问题的解。具体的，记： 有以下定理：

  • 对于 ，有 。

  [Admitted]

• 在以上的保证下，主要的问题是求解嵌入 ，对此有两条路线，盲式构造（oblivious）与依赖式构造（non-oblivious）。前者的思想是，构造 的分布 ，使得对于任意列满秩的 均有： 其中 是一个大常数，例如 。而后者的思想是对 进行适当的行采样。

盲式稀疏子空间嵌入

• 此处对于 的构造方式是为每列独立均匀的选择 个位置，并独立随机的填入 ，在其它位置置零。¹该方法被称为 OSNAP（Oblivious Sparse Norm-Approximating Projections）。

  OSNAP 的主要问题应该是证明其嵌入的正确性。已有的结果包括：

  

• 另外一个有趣的情形是 的情况，此时 被称为 Count-Sketch 矩阵。²已有的结果是当 时可以满足嵌入的性质。³这使得计算 时仅需 的时间，开辟了 input-sparsity 时间算法的研究方向。

Importance sampling 与杠杆值

• 这是本文的重点。依赖式子空间嵌入的基本思想是 Importance sampling ，即以概率 保留 的第 行，并乘系数 ，其中乘系数的目的是做归一化。若记提取行操作的随机嵌入矩阵为 ，就有： 具体的，我们希望保留的维（行）应满足存在 使得 相较 整体为大。这是一个直观的想法，因为我们若要对范数做近似，自然应该关注对范数的影响最为显著的维。为此，定义杠杆值 使得： 再令 即可。现在令 为 的列空间的标准正交基，我们就有 ，其中 为一满秩方阵。那么： 注意到分子分母是齐次的，因此我们要求 ，这样就有： 其等价于 的第 行到 所在方向的投影，从而不超过 的第 行行向量的范数平方。现在考察 ，其恰为 的全体元素的平方和，等价于列向量的范数平方和，从而恰为 。

• 由以上的讨论，也可以看出 不依赖于具体的 ，而是 的列空间的固有性质。另一方面， 亦描述 的第 行被其它行线性表出的难度，即有： [Admitted]

行采样导出子空间嵌入

• 应用杠杆值加权，我们期待可以得到好的嵌入，这就是以下的行采样定理：
  • 对于列满秩的 ，其杠杆值为 ，令 [^4]， 。对于对角阵 ，有： 那么以至少常数 的概率有：
  这样做的好处是， 应当是一个相当稀疏的矩阵，以大的概率其非零行数为：

• 现在我们给出行采样定理的证明。对 做常数因子的缩放后有： 任取 的列空间的单位正交基 ，可得 ，其中 为满秩方阵，则只需： 进一步对对称阵 做特征值分解得到 ，上式又等价于： 容易看出这意味着所有的 。记 的第 行对应的列向量为 ，则对于随机变量 ，有： 这是对称随机矩阵的和，适用 Bernstein 不等式，我们先给出其叙述：

  • 对于独立随机对称矩阵 ，使得 且 。令 ，则对任意 有： 此处对于对称阵 定义其范数为 。

  [Admitted]⁴

  令 ，容易看出 。现在考察 的特征值，应有： 令 与 平行，立刻得到 ，并且由于 实对称，其余的特征向量应与 正交，这说明它们的特征值均为 。从而 。另一方面，注意到 ，从而：⁵ 再由 Bernstein 不等式： 而右式为一常数，令其为 即可。

• 另外的一个重要看法是，以上方法的采样行数为 ，其中的 是有必要的。因为若构造 使其为 个 单位阵的堆叠，则对其杠杆值的行采样服从均匀分布，按照 coupon collector 模型，期望需要 次才能覆盖所有行。

杠杆值的计算

• 考虑计算 ，若采用准确的方式，如 Gram-Schmidt ，需要 时间，这意味着我们可能需要同样对 做近似。至于具体的过程，这里就不再详述了。另外 lecture 后面还有一些更深入的内容，限于作者水平，我们也就不写了。

---

1. 注意到 恰为 的逆即可。↩︎

2. 这个名字应该是某种拿来主义。↩︎

3. Clarkson-Woodruff'13, Li-Liu'22↩︎

4. 这个我还真不一定会证。↩︎

5. 这里我省掉了一部分推理，因为我其实并不熟悉矩阵概率，先承认吧。↩︎