熵的性质

熵有一些显然的性质，例如其是凹函数，这里就不赘述了。下面我们将定义一些其它种类的熵，并介绍其性质。

联合熵

• 对于对于随机变量 ， ，假定其联合分布服从概率质量函数 ，则其联合熵为：¹ 简单地说，把 视为随机向量即可。按熵的定义，可以验证一些简明而深刻的性质：

  1. 若 ，则 ，即 不会引入新的不确定度。
  2. 若 ， 。

条件熵

• 随机变量 的条件熵定义为：² 可以验证：

  1. ，当且仅当 。

  2. 。

  3. 条件熵的链式法则：

相对熵

• 不同于之前，相对熵这个概念其实是对于同一样本空间的不同分布谈的。考虑以下问题：假设我们希望对包含 个文字的语言编码，但是我们无法观测到文字的真实分布 ，所以我们希望通过某种方式，例如采样，来估计 ，从而得到了某一近似的分布 。现在我们希望估计 逼近 的好坏，具体的方式则是计算用 编码的期望码字长度与用 的差。我们知道真实的最优期望长度，对应熵，是： 而用 编码的期望长度则是：³ 特别的，上式也称作 与 的交叉熵，这里记作 。容易计算得到： 我们就将右式定义为 到 的相对熵，记作 。先前我们证明了熵编码的最优性，因此 。相对熵可以被用来度量分布的相似度，但严格的说其并不是“距离”，因此其不满足对称性。有些时候我们也拿交叉熵来替代相对熵，因为在固定 时 是常数。另外相对熵也被称作 KL 散度，但是我不知道“散度”这个名词到底有什么深刻的含义。

  另外相对熵也有一些性质：

  1. 链式法则：

互信息

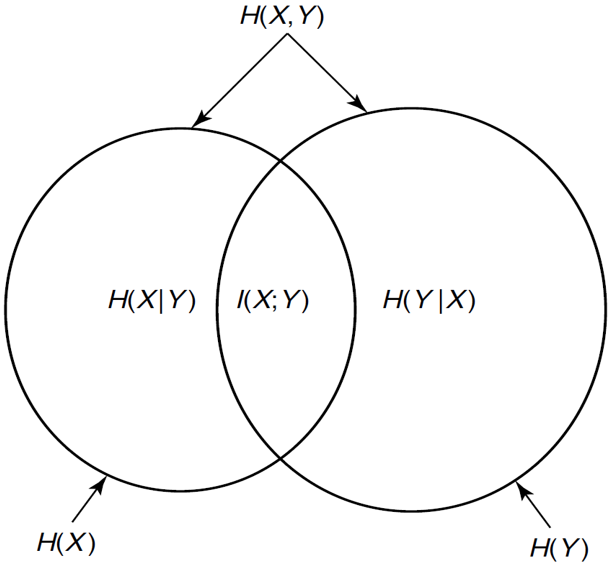
• 随机变量 的互信息定义为： 可以认为互信息度量了用 独立的假设估计其联合分布的准确度，但一个更有趣的观点是： 即 度量了 和 ​ 的信息量的重叠部分。如果使用韦恩图表示熵的关系，可以得到：

  

  这是一个非常有趣的事实，其说明我们的确可以期待熵在一定程度上表述了随机变量的信息量。

  另外互信息还有一些性质：

  1. 若 ，则 。

  2. 链式法则：

  最后，你可能会对以上的这些记号与它们的性质感到困惑，但总体来说，它们之间的关系还是相当简明的。我们说过，“熵在一定程度上度量了随机变量的信息量”，而以上的这些定义就在某种程度上概括了随机变量蕴含的信息的交、并、差关系。我们可以把随机变量的信息量视作集合，将条件熵作差、联合熵视作并，互信息视作交，这样以上的性质就都非常符合直观了。⁴

---

1. 这里的 代表 的样本空间。↩︎

2. 下面的概率的记法可能和概率论有些不同。↩︎

3. 真实分布不会改变，改变的只是我们设置的编码长度。↩︎

4. 严格的说，该线性关系和集合之间的关系的确是一一对应的，但是在更复杂的情况下每个区域对应的量不一定是正的。证明参见 Ch. 3, Information Theory and Network Coding, R. W. Yeung↩︎