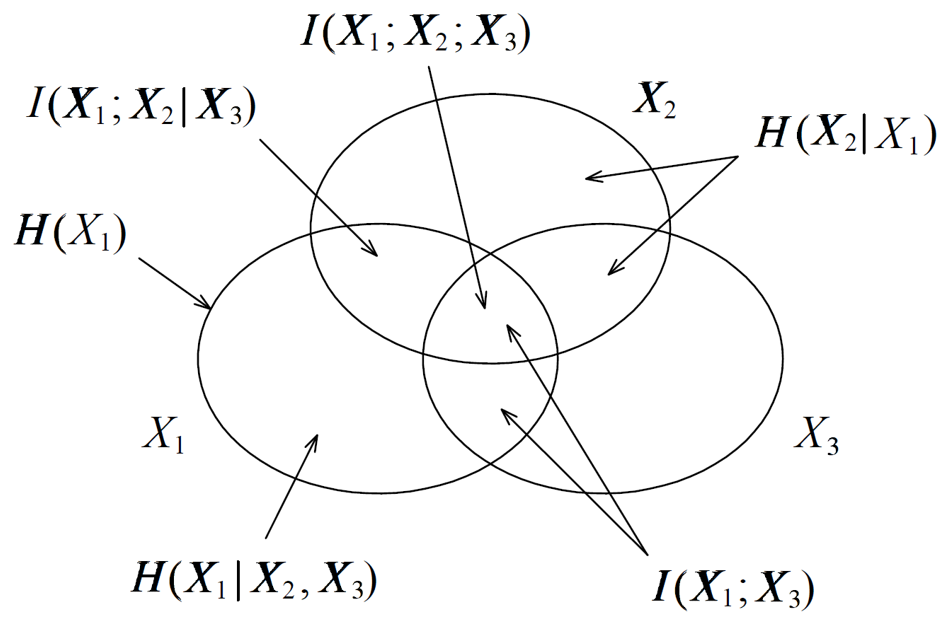马尔可夫链与法诺不等式

下面我们将简要介绍 Markov chain 与 Fano's Inequality 。

马尔可夫链与数据处理不等式

• 理论上马尔可夫链在信息论的先修课概率论里应该是讲过的，但是由于我自己没有学过，所以这里还是简述一下。我们称一列随机变量 构成马尔可夫链，记作 ，当且仅当随机变量的条件概率仅依赖于其前驱。即： 容易验证：

  1. 在三变量时马尔可夫链是可逆的，即 。
  2. 。

• 数据处理不等式是马尔可夫链的重要性质。即： 证明比较简单，对 用链式法则拆出马尔可夫链的形式即可。另外还有： 而在一般情况下上式是不一定成立的。¹但我们还是定义： 这样可以画出三变量的韦恩图：

  

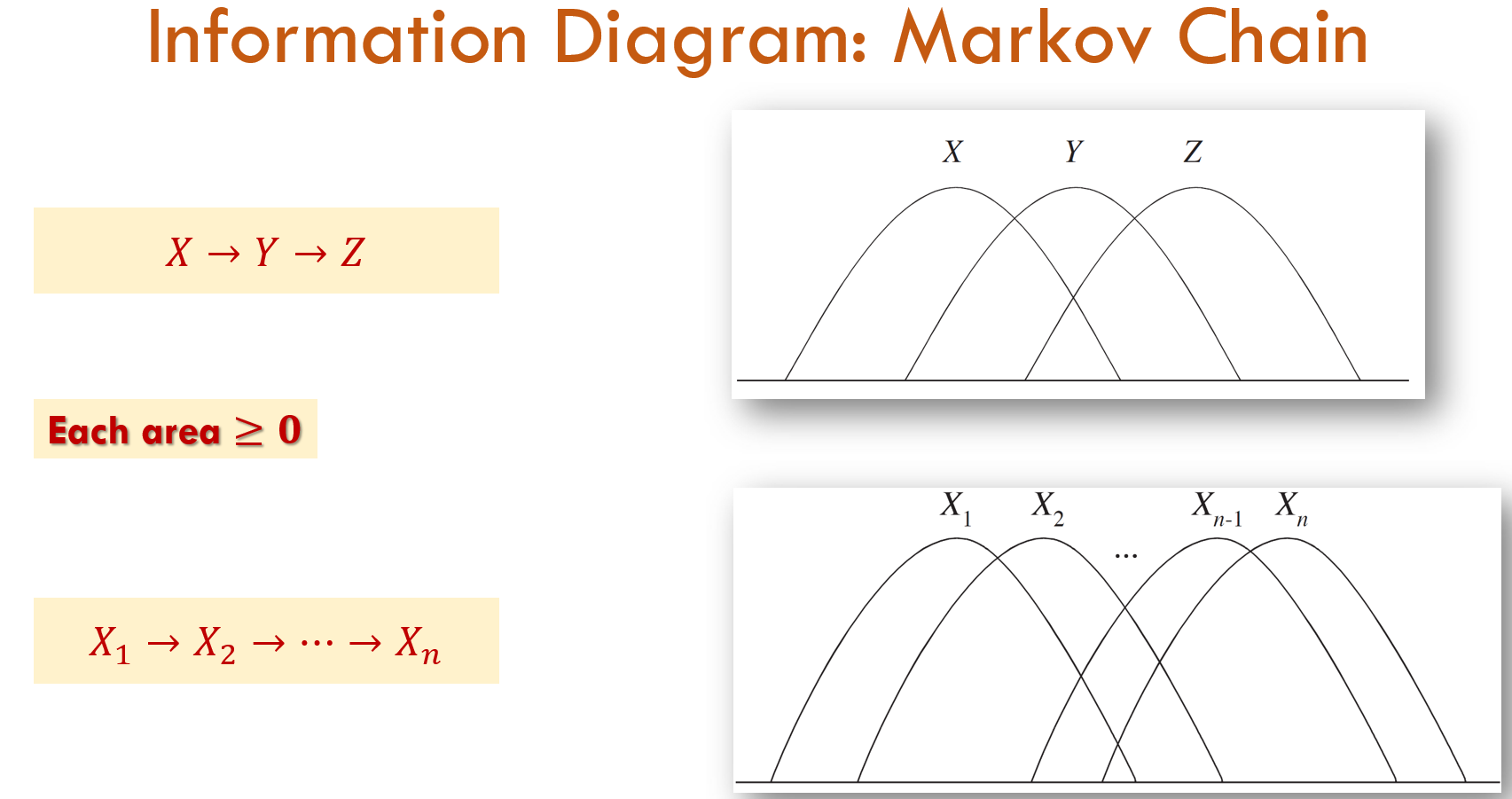
  各部分的线性关系仍然符合一般的集合运算，但是中间的三变量互信息不一定是正的。而马尔可夫链的韦恩图就要简单很多，而且保证每个区域对应的量都是正数。（分布式加密的例子后来补上）

  

法诺不等式

• 考虑以下模型：给定信源 ，我们将 编码，并考虑噪声的影响，得到传输信息 ，然后我们希望通过解码 恢复 。由于噪声的存在，完全恢复 很可能是做不到的，我们只能对 做估计，从而得到 。注意到这个过程形成马尔可夫链： 现在，我们希望衡量解码错误的概率。为此，定义错误指示变量 使得 ，令 。为了利用马尔可夫性，考虑： 注意到：

  1. 。

  2. 。

  3. 考虑：

  因此： 这就是法诺不等式。现在我们希望放松法诺不等式来估计 ，即： 这是一个很有用的工具，因为后面要提到的信道模型是符合我们一开始的马尔可夫链建模的，所以我们经常使用法诺不等式来估计信道错误的概率。

另外的一些不等式

• 好像意思不大。以后再补。

---

1. 直观上因为互信息不度量不确定度。↩︎