浅谈强化学习的深度学习方法

本文将引入强化学习这一领域，并简要介绍一些基础的理论建模，及其深度学习的解法，例如 Deep Q Learning 和 Policy Gradient 。

问题背景

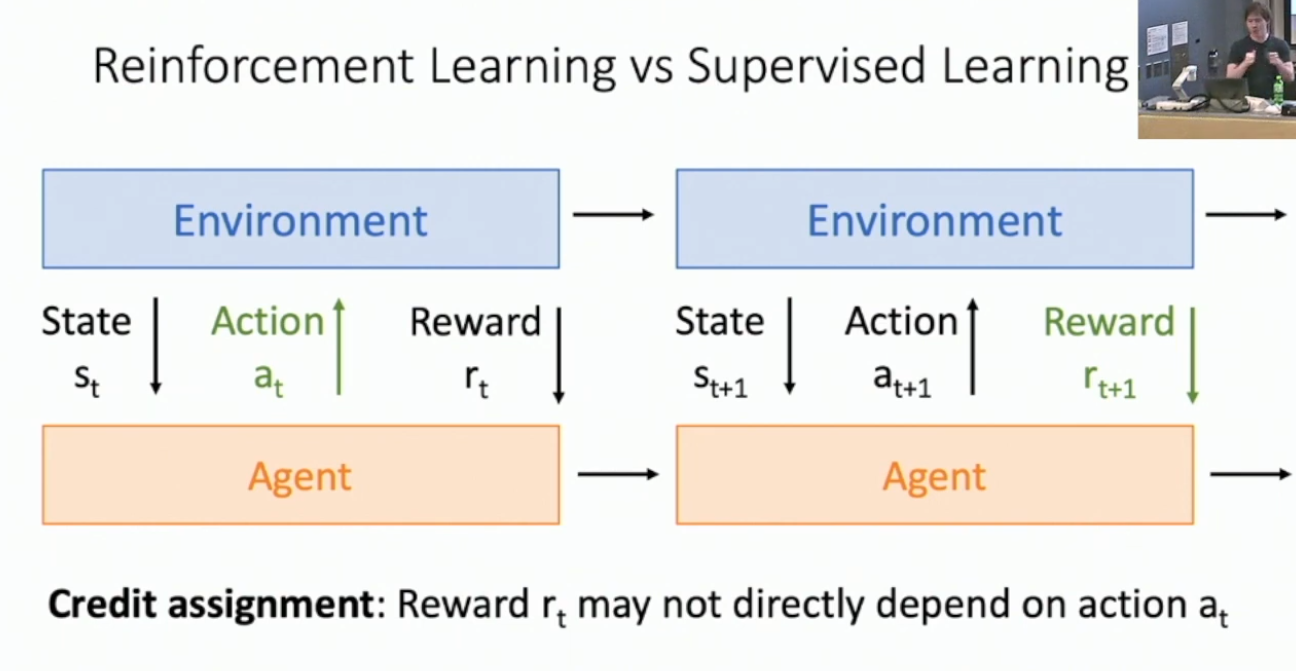
• 总的来说，强化学习是一个相当难的问题，显著的难于我们之前所建模的问题。简单的说，强化学习的目标是训练一个依据某种规则与外界交互的模型。一个合理的建模是，设想存在某个外部环境，以及某个我们希望训练的模型。该模型每次从环境中获取当前环境的状态 ，然后做出自己的行动 ，该行动对环境造成影响，同时环境要向模型发送奖励 。接下来环境和模型都会变化，并进行下一轮交互，以此类推。

  

  你可能会觉得这个问题建模看起来和之间的监督学习有点像，因为监督学习反正也是模型和数据集交互。但强化学习有一些本质的困难之处，例如：

  1. 随机性。环境可能会随机改变。
  2. 我们可能不知道是哪一步行动导致了当前的奖励，即奖励会受先前的行动影响。
  3. 不可微。先前的模型中我们总是希望通过梯度手段来调整模型，而强化学习的过程不一定是可微的。
  4. 环境不稳定。随着模型的行动，外界环境可能会发生较大的改变，导致模型先前收集到的信息、学习到的方式难以适用于新环境。更严格的说，外界环境对应的分布不是一个稳定的分布。

马尔可夫决策过程与 Deep-Q Learning

• 现在我们将简要介绍强化学习的数学建模之一，马尔可夫决策过程。我们使用一个 元组来描述马尔可夫决策过程的状态空间，即 ，其中：

  • ：环境的所有可能状态的集合。
  • ：模型的所有可能行动的集合。
  • ：给定 时奖励的分布。
  • ：给定 时，下一步转移到的状态的分布。
  • ：衰减系数。

  特别的，我们要求当前状态 完全描述了外部环境，即给定 时分布 和 就完全确定了。我们将该性质称作马尔可夫性。我们的目标是让模型学习某一策略 ，使其最大化长期的收益： 其中 代表第 步的奖励， 即为衰减系数。因此，衰减系数的作用主要有两个，其一是使得模型在一定程度上更为关注较近的奖励，其二也潜在的帮助长期收益收敛。而模型在马尔可夫决策过程中的行动模式则是：

  • 当 ，环境从给定的初始的状态分布，记作 ，中取样，得到初始状态。
  • 接下来，模型不断重复：
    • 模型根据策略 ，从分布 中取样得到当前行动 。
    • 环境从分布 中取样得到当前奖励 。
    • 环境从分布 中取样得到下一状态 。
    • 模型接受奖励 并转移到下一状态 。

  当然，这是一个随机过程，所以我们无法期待稳定的收益。因此，我们的优化目标应是给定策略 时的最大期望收益，也就是： 在给定策略 时，我们希望衡量某一个状态的优劣，为此我们定义价值函数： 有时我们希望衡量在当前状态 下采取行动 时的收益，为此进一步定义 函数： 现在我们考虑最优的 函数，即： 现在我们就要做一些假设了。¹一般来说，我们认为 应是一个分布，然而此处我们假设每一步仅做确定性的选择，即令 为一 的函数。这样，我们可以期待： 现在考虑如何求解 ，我们期待 满足递推关系，而这一点其实应该是有保障的，即如下的 Bellman Equation ： 其中 。实际上我们期待 Bellman Equation 满足一些更强的性质。我们不加证明的给出：²

  • 对于任一满足 Bellman Equation 的 ，其必然恰为最优的 。

  • 考察函数列： ，其中 为任意 ，满足： 有 一致收敛到 。

  要求解 ，一个简单的思路是我们直接按照如上性质，从任意初始函数开始做迭代。然而 的定义域可能很大，使得这一方法无法实现。此处我们考虑引入神经网络来预测 ，并使用 Bellman Equation 作为损失函数。即，假设我们使用参数为 的网络预测 ，得到 。考虑： 我们期待 ，即设定损失函数为： 其中的期望则通过对 做取样来近似。当然，以上的叙述仍是相当粗糙的，有一些比较重要的技术细节，例如如何选择训练时的 mini batch 、如何取样，我们都不会在这里深入。不过以后我们可能会考虑以 Alpha Zero 为例来实现 MCTS + Deep-Q Learning 。

策略梯度方法

• 在以上的 Deep-Q Learning 中，我们假设了 ，并使用函数 来描述 。这样，我们可以通过学习 来间接的学习 。而此处的 policy gradient 则更加直接，即我们希望通过某种方法直接学习 的分布，具体的手段是使用神经网络和梯度方法。具体的，我们考虑训练一个模型，使其对于输入的状态 ，预测策略的分布 。记模型参数为 ，则由这些参数所描述的策略的期望收益为： 我们希望通过梯度上升来调整 从而最大化收益。即： 我们会采取对实际行动做有限的取样来近似期望，然而取样过程是不可微的，因此我们需要一些技巧。我们考虑由参数 所指定的，状态与行动序列 的分布 。我们有： 考虑： 假设求导是可交换的： 注意到： 因此： 进一步： 这是一个相当好的形式。具体的，设想我们通过若干次对行动序列取样来近似期望。在每一次取样中，我们进行有限步行动。其中 可以在取样时计算；并且每当我们使用模型预测 ，我们都对 进行反向传播以计算其梯度。这样，我们就得到了可微的最终形式，使得我们可以用梯度方法来优化 。³

  当然，Policy Gradient 方法还有一些潜在的技术细节，这里无意深入。

---

1. 尽管 Justin 在他的课上没强调这些，但我认为这些数学上的细节还是值得一提的。说实在的他在课上也没有非常严格的谈这些，毕竟这不是正经的 RL 课。↩︎

2. 可能不是很严谨啊。↩︎

3. 特别的，奖励和状态的分布 和 我们实际上都是不知道的，我们只能对其取样。而 Policy Gradient 的一个好处是，其通过对 求导这一操作避免了计算 的分布。↩︎