生成模型：自回归模型、变分自编码器与生成对抗网络

本文将引入一个新的研究分支，即生成模型，并且将简要介绍其中的自回归模型、变分自编码器与生成对抗网络。

问题背景

• 为了介绍生成模型与先前的分类模型的区别，我们需要先介绍一些基本概念。

  • 监督学习与无监督学习：简单的说，监督学习需要人工标注数据，而无监督学习则不需要。举例来讲，我们先前所讨论的所有深度学习模型都是监督学习；而聚类或者编码器这类模型则是无监督学习。一般来说，比起监督学习，我们更喜欢无监督学习，因为其不需要人工标注，所以可以方便的使用大量数据训练。

  • 判别模型与生成模型：判别模型与生成模型的区别是，它们所要学习的概率模型是不同的。¹对于数据点 与标签 ，判别模型要学习的分布是 ，即，给定 时 的概率质量函数。一般的生成模型则直接学习数据点的分布，其概率密度函数记作 。²这就是说： 而条件生成模型则是对于每一个给定的标签学习其条件密度函数 。我们可以看出，判别模型用于判别给定数据点的标签，但其并不能很好的剔除 outlier（不满足任何一类标签的数据），因为各标签的概率之和总为 。生成模型可以用于从数据点的分布中采样，也就是生成新数据。而条件生成模型也可用于判别任务，并且可以剔除 outlier ，即那些在所有标签上概率密度都很低的点。

    另外对于条件生成模型，我们一般应该不会考虑对于每一个标签分别训练，而是使用贝叶斯公式： 其中分子部分分别对应判别模型和生成模型，而分母则是标签的先验，一般使用频率估计。

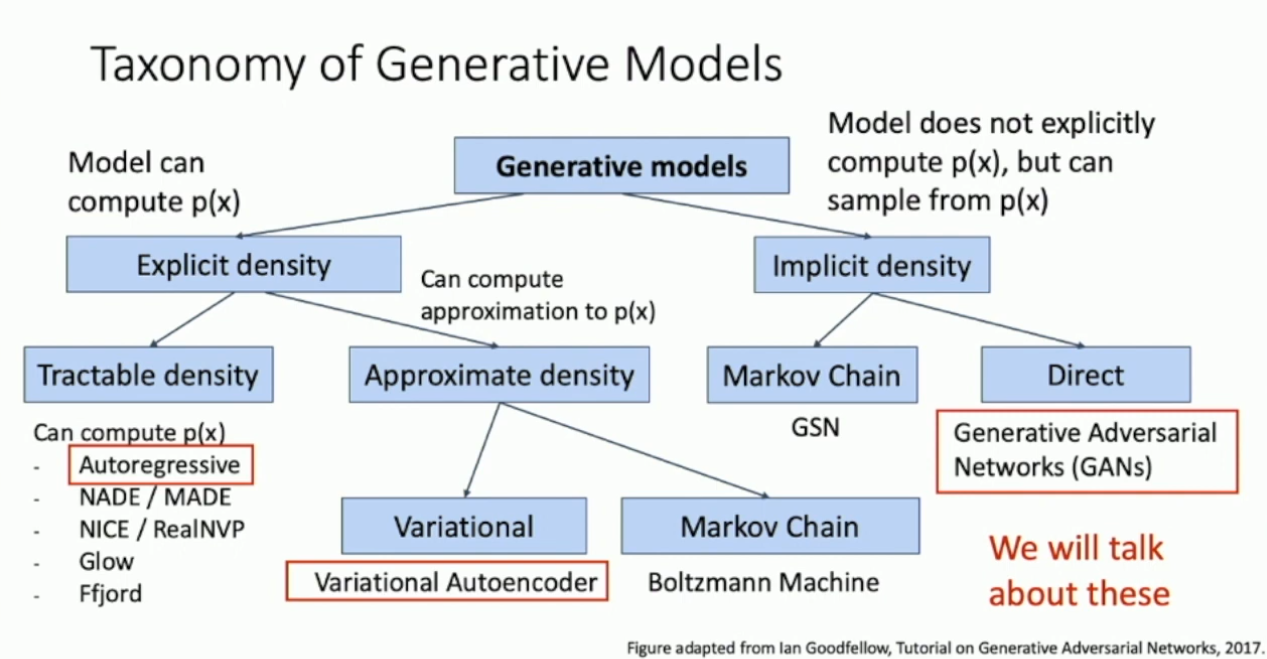
  所以本文将要介绍的生成模型，区别于先前所述的判别模型，其主要任务是学习数据点的分布并从中采样，也就是生成新数据。生成模型有很多细分模型，下图展示了一个简要的分类：

  

  本文将着重介绍其中的 autoregressive model 、Variational autoencoder 和 Generative adversarial network 。

自回归模型

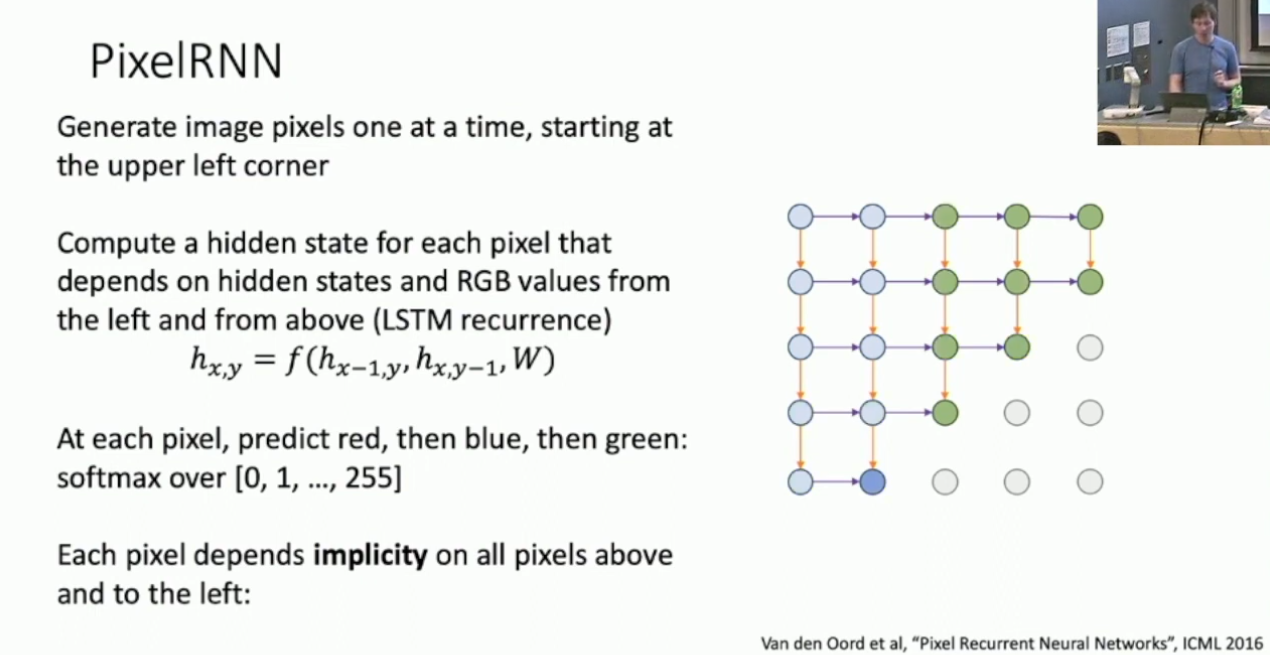
• 简单的说，autoregressive model 希望通过给定的数据点直接学习数据的分布，并显式的给出其概率密度函数。对于数据集 ，假定数据采样是独立的，那么该数据集的概率是： 假定 服从参数为 的分布，其概率密度函数为 ，我们希望最大化其似然： 对于 ，假定其有 个分量 ，则： 这就是说每一个 都只依赖于其前缀，所以我们考虑使用 RNN 来建模这个模型。³具体的，对于图像生成模型，我们考虑 Pixel RNN ，即对于位于 处的像素 ，有： 这样，按照上述方式建立 RNN 即可，而每一个像素依赖于其左上的所有像素。

  

  然而 Pixel RNN 具备时序依赖而难以并行化，因此另一个方式是 Pixel CNN ，这里无意深入。其大致的思想是使用 CNN 来进行预测，从而使得训练时可以并行化，然而推理时仍然是时序依赖的。⁴

变分自编码器

• 以下我们将简要介绍变分自编码器的原理和应用。

自编码器

• 我们先介绍自编码器这一概念。本质上，自编码器用于进行特征提取，如同我们先前介绍的用于特征提取的 CNN 一般，区别在于自编码器是无监督的。简单的说，我们先构造一编码器，用于将输入压缩成较小的特征，再使用解码器将特征重建成输入。我们会同时训练编码器和解码器，而因为我们只需要比对输出和输入的相似性⁵，因此并不需要做任何的数据标注。在训练完成后，我们将丢弃解码器，而在编码器后追加额外的结构，比如一个分类器，来执行其它任务。值得一提的是，尽管编码器是一个看起来很棒的概念，它在实践中的效果往往不如监督式的特征提取器。

  另外自编码器并不是基于概率的模型，所以其不能用作生成模型。⁶

变分自编码器的原理

• 而变分自编码器则要为编码器引入概率建模，从而使得我们可以从中采样。具体的，首先我们要引入一些假设。假定特征空间中的特征 服从某个概率分布，数据空间中的数据点 服从另一个概率分布，并且这两个分布并不是独立的。我们希望训练一个模型，称作解码器，使得可以对于给定的特征 计算给定 时 的分布。

  以上条件还不足以我们建立具体的模型，所以我们要加强一些条件。具体的，我们假设 和 都分别服从独立高斯分布，之所以要求独立是因为协方差矩阵太大而无法处理。在训练时我们只能得到数据点而无法得到特征，所以我们考虑最大化数据点的似然： 我们希望建立数据点与特征的关系，考虑贝叶斯公式： 其中 是任取的。我们假设 服从一个简单的先验的分布，例如单位高斯分布，而 则由解码器预测。所以问题出在 上，这一项是没法算的。为此，我们考虑用另一个模型，称作编码器，来预测 ，从而得到另一个相似的概率密度函数 。你可能会想直接用 替换 来计算似然，但这样做太糙了。为了估计得更精细，现在我们要稍微推点式子： 注意到 与 无关，所以 。这样： 如果你有一点信息论基础，应该可以看出后两项形式上都是相对熵，因此都是非负的。对于最后一项，其包含了无法计算的 ，所以我们将其丢弃，就得到了： 我们无法直接优化似然，所以我们考虑按照上式优化似然的下界，这样就得到了如上的目标函数。而具体的训练过程则概括如下：

1. 对于数据点 ，将其输入编码器，得到概率密度函数 ，其服从独立高斯分布。
2. 使用 和 计算目标函数中的相对熵部分。⁷
3. 从 进行采样，得到若干 。
4. 将上一步得到的 输入解码器，得到 。
5. 使用采样得到的 计算 的均值以估计 。

而在采样，即生成图像时，我们将丢弃编码部分，直接从先验分布中对 采样，再将其输入解码器，得到生成图像。这样搞看起来不是很有道理，因为其采样得到 并不直接服从 的分布。也许可以认为我们对 的采样是在选择类别，而解码器则是在该类别中生成具体的图像。⁸

变分自编码器的应用

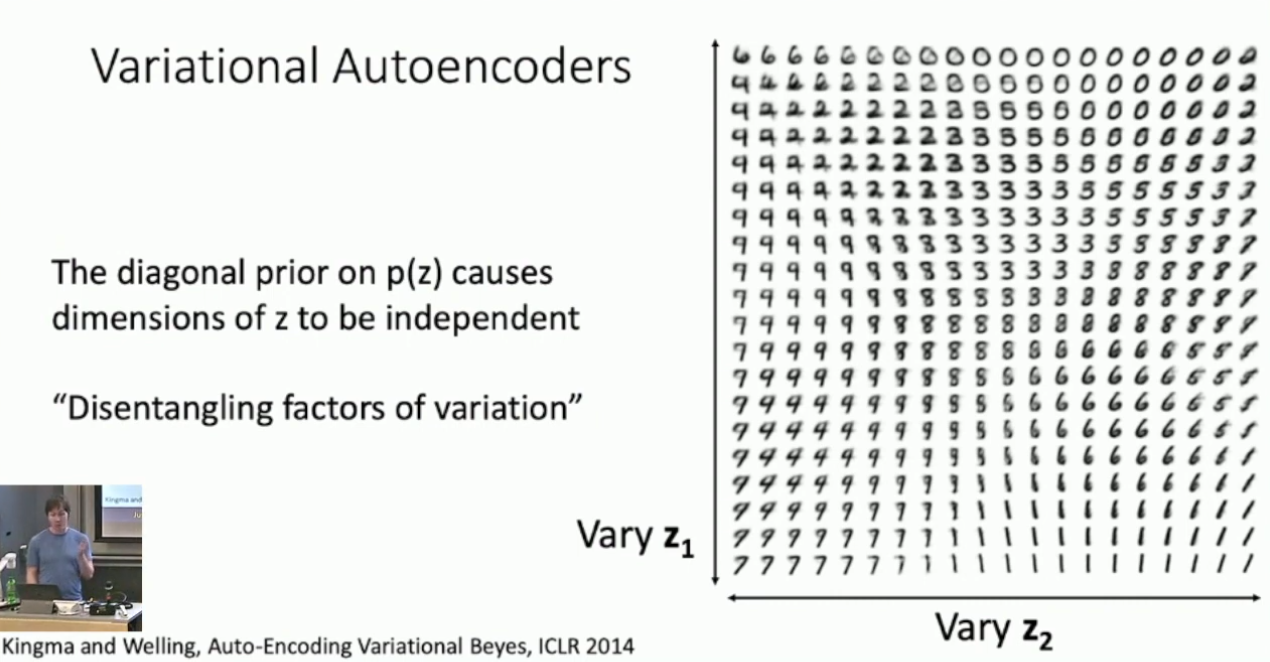
• 变分自编码器有一些非常有趣的特性。因为特征 服从独立高斯分布，所以我们可以期待 的每一维都编码了特定的信息。举例来讲，对于 MNIST 上训练的 VAE ，若改变其特征 的两维，我们可以期待看到这样的效果：

  

  即 的不同维度编码了数字的某种相似关系。另外，我们也可以考虑将特定图像输入编码器得到其特征，再改变该特征的特定维度，我们可以期待看到如下的结果：

  

  即，特定的维度编码了面部的朝向和表情信息。然而需要指出的是，我们很大程度上不能预测这些维度上到底会编码什么东西。

生成对抗网络

• 以下我们将简要介绍 Generative Adversarial Network 的原理及应用。

生成对抗网络的原理

• 不同于先前所介绍的模型，GAN 不关注对分布建模，而只关注取样。具体的，假定随机变量 服从数据点的真实分布，我们对其取样得到了 个样本 ，而我们的目的是从真实分布中采样。形似 VAE ，我们设置特征 ，并令其服从某个简单的先验分布，例如单位高斯分布。接下来，我们希望训练一个生成网络，将其视作一个函数 ，使其作用于 ，得到代表数据点的随机变量 ，我们希望 可以近似真实分布。

  与此同时，我们希望训练另一个辅助模型，称其为判别网络，使其可以判别给定的数据点是真实的，还是生成的。判别网络将会在生成网络和数据集上同时训练，我们期待当训练一定实践后，生成网络和判别网络都迭代得足够好，使得生成网络可以生成相当逼真的数据。

  当然以上所述实际上并不能保证 真的会逼近真实分布，这一点其实是由目标函数保证的。我们将判别网络视作一个函数，其将数据点映到 ，也就是其为真的概率。那么目标函数为： 其中期望应该是通过对 的样本和 采样来估计的。下面我们希望说明上述目标函数达到最优，当且仅当 和 同分布。注意到 和 的值域相同，则： 假设这些函数的性质足够好使得积分和 可以交换⁹。那么： 再假设对于任意的 ， 可以在 间任取，则容易得到上式 内的部分的最优解在： 时取得。从而： 可以看出上式的两个期望都是相对熵，因此是非负的，并且当且仅当 时（若可以取到），它们的和取得最小值 。这就说明原目标函数（在以上的假设下）取得最优解时必然有 和 同分布。

  另外还有一些技术上的细节。首先因为优化目标是一个 minimax game ，优化时的曲线并不一定是单调的，这会使得优化更难。另外的问题是，在最初的迭代当中，判别网络应该很容易分辨出生成网络的输出，所以 基本是 ，而 在 处的导数值是较小的，所以可能产生梯度消失问题。因此在训练时可能会考虑把 换成 。¹⁰

生成对抗网络的应用

• GAN 还有一些非常有趣的特性，其特征空间的结构其实是非常微妙的。举例来讲，如果我们从 GAN 的特征空间取样得到两个点，再对它们做插值¹¹，那么其实可以看到插值点生成的图像的平滑变化。

  

  另外一个更厉害的特性是，我们甚至可以直接用特征做加减法。比方说，我们希望对具备“戴眼镜的男人”、“不带眼镜的男人”、“不戴眼镜的女人”这几个标签的特征采样，对每一类特征平均，再令第一类特征的均值减去第二类特征、加上第三类特征，从而得到具备标签“带眼镜的女人”的特征。这种事看上去很蠢，但令人震惊的是，我们其实真的可以这样期待。

  

  我们也可以构建 Conditional GAN ，即对 GAN 的概率建模引入标签。而对应的技巧其实在用 CNN 做 style transfer 的时候介绍过，就是在 Batch normalization 的时候对于每一个标签分别维护其常数因子和偏置。另外 GAN 还有一些非常有趣的应用，例如超分辨率、文生图、视频生成、等等。GAN 的应用其实非常多，其可以用来建模很多问题，并且还是（截止2019年）的热点之一，这里也就不再深入了。

---

1. 生成模型的本质其实不像是生成，而是从概率分布中采样。↩︎

2. 如果只考虑位图的话全体图像其实是有限的，不过我们这里还是考虑无限的情况。↩︎

3. 好像也没什么理论上的具体的道理。↩︎

4. 技术细节参阅原论文。Van den Oord et al, Conditional Image Generation with PixelCNN Decoders, NeurIPS 2016.↩︎

5. 使用 范数之类的。↩︎

6. 我猜如果我们考虑做特征采样，再将其输入解码器，那么绝大多数时候我们都可能会得到乱码。因为实际上在特征空间中，只有较小的一部分点对应了有意义的图像。↩︎

7. 如果你愿意推点式子，这个部分其实是具备封闭形式的。↩︎

8. VAE 有一个很大的问题就是生成出来的东西太糊了。而一个有趣的改进，称作 VQ-VAE2 ，似乎显著的改进了 VAE 生成的图像质量，其主要思想是在 encoder 和 decoder 之间引入自回归模型对特征做调整。这里无意深入介绍，详情参阅 Razavi et al, Generating Diverse High-Fidelity Images with VQ-VAE2, NeurIPS 2019.↩︎

9. 这个条件其实很严格啊。但是假定概率密度函数存在这件事应该也挺严格的。说到底这种地方也没法谈严谨性。↩︎

10. 理论上 在 处也是有梯度的啊。不知道为什么这里又要求这么大的梯度。↩︎

11. 即 interpolation 。我没在其它地方看到过这个叫法。其实更像是凸组合。↩︎