注意力机制

RPChe_
  2025-03-18 2025-03-18 创建   2025-03-19 00:55:44 2025-03-19 00:55:44 更新    2.1k 字  7 分钟  

Attention Is All You Need.

问题背景

  • 我们将主要讨论处理有关序列问题的技术，包括但不限于

    1. one to many: Image Captioning.
    2. many to one: Video Classification.
    3. many to many: Machine Translation, Video per-frame Classification.

    而本节的主线将着重于 Machine Translation 。

算法描述

  • 本部分将介绍 Attention 在不同模型中的使用。

Attention for RNN with Machine Translation

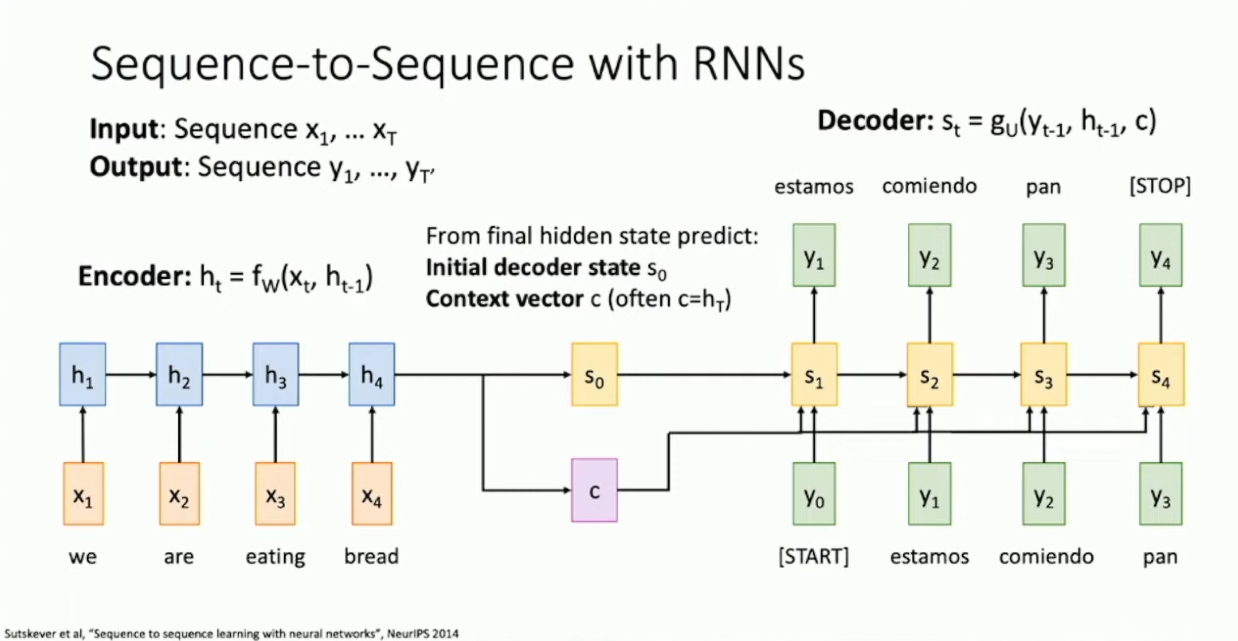
  • 不妨先想想先前 RNN 是怎么处理 Machine Translation 的。考虑下图的模型：

    我们使用了一个 encoder RNN ，将输入的内容压缩成了一个 hidden vector ，然后我们使用 通过某种方式（例如一个前馈全连接神经网络）生成了 decoder 的初始状态 ，并保存 作为 decoder 的 context 。接下来，我们使用新的 hidden vector 、context 和上一步的输出参与下一步的计算。1

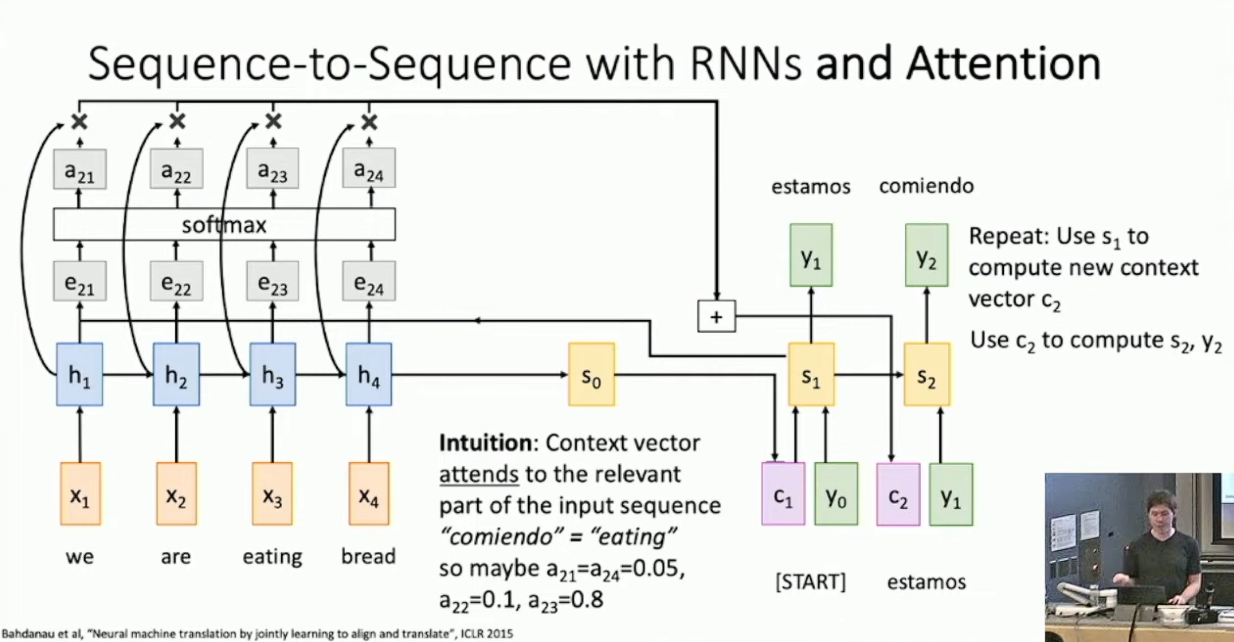
    这样设计会有一个问题，我们实际上将所有的信息都打包进了单个 context vector 当中。当输入的文段很长时，我们其实不能期待这样的一个向量可以表示全部的信息。为了提供更多的信息，我们试着不再用单个向量来表示所有上下文，这就引入了所谓的 Attention 。具体的，我们考虑设计一个 alignment function（ ，可能是一个全连接网络），用以评估 与先前的所有 的关系，计算得到一个权重，表示为： 然后我们将所有 通过 softmax2 计算得到一个分布 ，做 对于 的加权和得到向量 ，并将其作为当前的 context ，参与下一步的计算。大体过程如下图所示：3

    我们期待这样做可以提取出输入中显著影响下一步预测的组分，凸显输入的影响。作为例子，下图展示了机器翻译中每一步 attention 所计算出的分布：4

    这的确展示了不同语言中词汇的对应关系。

Attention for CNN with Image Captioning

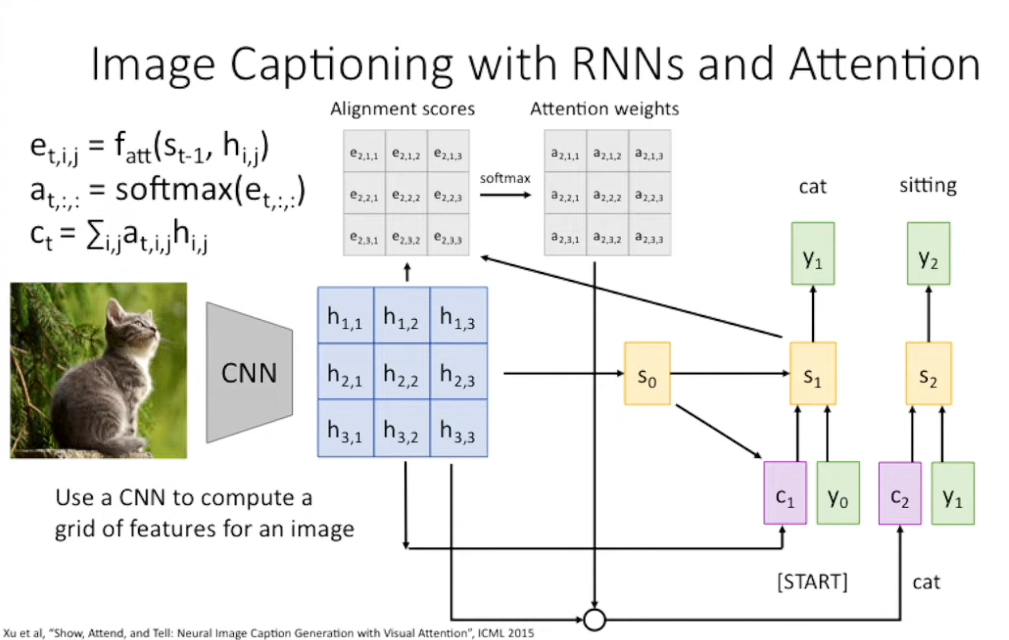
  • 你可能已经注意到 Attention 本身其实并不依赖于序列或者 RNN ，我们只是对代表不同组分的向量做加权和而已。所以 Attention 也可以被无痛迁移到做 Image Captioning 的 CNN 上。我们直接给出网络的结构：

    这是一个迁移学习的框架，我们组合了 CNN 和 RNN 用于 Image Captioning 。具体的，先在 Image Classification 上预训练出用于特征提取的 CNN ，我们期待最后 CNN 的每一个 feature vector 都表征了原图像的一部分视野。那么，我们可以对 feature vector 使用与原先基本相同的注意力机制来提取图像中与 RNN 的下一步预测相匹配的位置。56

Attention Layer

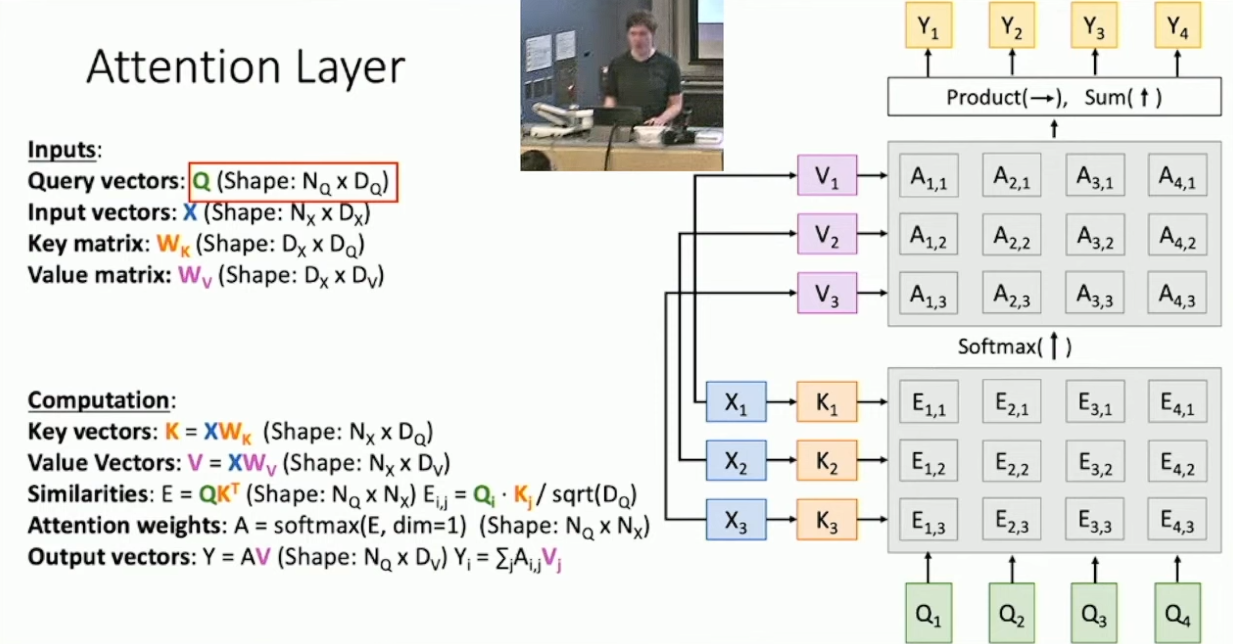
  • 既然 Attention 这么好用，不妨考虑将其剥离出来，形成单一的 Attention Layer 。不妨想想 Attention 本质上做了什么：给定了 query vector 和 input vectors ，我们希望通过 alignment function 计算 相对于 的权重（相似度），并做加权和。简便起见，我们将 实现为向量内积。7这样做会带来一个问题，就是如果相似度太高，做 softmax 的时候可能会导致梯度消失，而维度越高，内积的项越多，值就可能越大。而解决方式是，我们考虑做对于维度的归一化操作，即做内积后再除以 的维度 的根。接下来，我们考虑 query vector 不唯一的情况，此时只需要改用矩阵形式即可。所以我们得到了：

    • For , calculate :

    • Similarities: , where .

    • Attention Weights: .

    • Output Vectors: .

    另一方面，注意到我们实际上用 做了两件事情，第一件是计算 input vector 与每个 output vector 的相似度，第二件是基于相似度对 做加权和得到输出。所以我们考虑将这两件事分离开，即基于 分别生成用于计算相似度的 Key vector 和用于计算输出的 Value vector 。过程如下如所示：

    这样我们就构造出了 Attention Layer ，其对于给定的 input vectors 和 query vectors 考察了前者对于后者的影响的重要程度。

Self-Attention Layer

  • 以上的 Attention Layer 总是要给定不同的 query vectors 和 input vectors 。有些时候我们希望考察输入的向量内部的关系，比方说我们希望理解一个输入的句子，这就引入了 Self-Attention Layer 。思路其实很简单，只需添加一个矩阵用以根据 input vectors 预测 query vectors 就行。8

    这样做会有一个性质，就是 Self-Attention Layer 对于输入向量具备置换不变性，但有些时候我们其实是希望关注输入向量的顺序的。解决方案是，为输入向量增加 positional encoding ，即给每个位置添加可学习的向量来区分位置，并把位置向量追加到 input vectors 的末尾。

    另一方面，有些时候我们并不希望之后的输入向量影响之前的输入向量9，相应的解决方案则被称作 Masked Self-Attention Layer ，其实就是强制把之后的权重全部置 0 ，将权重矩阵变成下三角矩阵。10

    另一个技巧被称作 Multi-head Self Attention Layer ，其实就是把输入向量拆成几节，每一节单独做 Self-Attention Layer ，最后再拼起来而已。这样做会引入一个超参数 num of heads ，另外 Self Attention Layer 内部还有一个超参数 ，称作 Overall Width/Size 。11

RNN, Self-Attention 与 Transformer

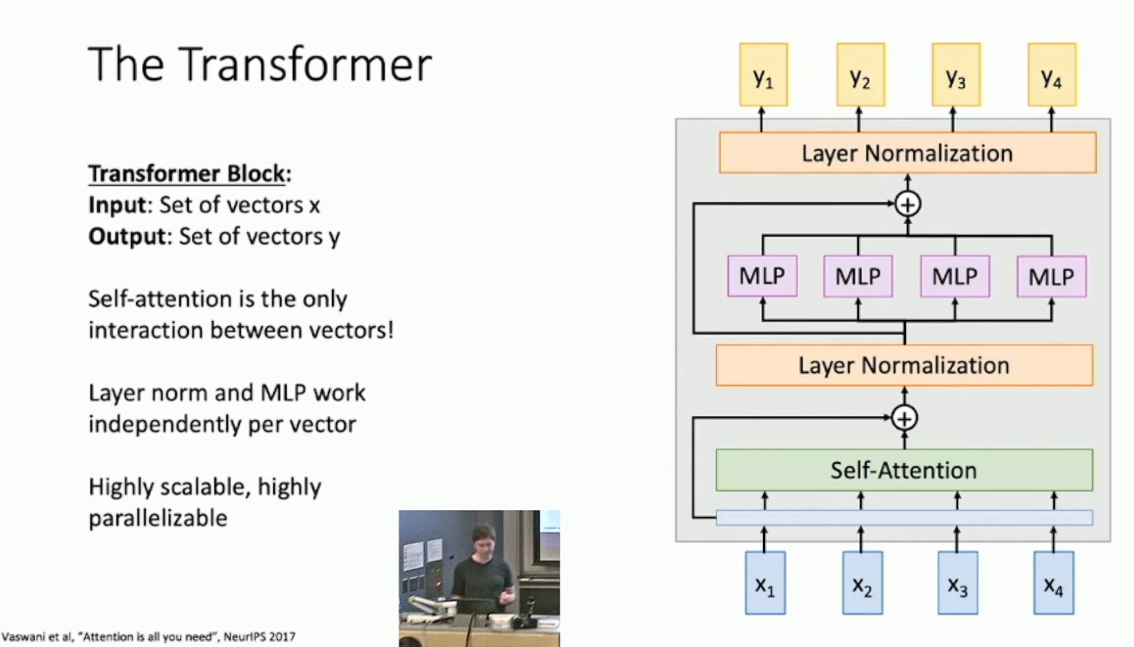
  • 总的来说，现在我们有两种处理序列的手段，分别是 RNN 与 Self-Attention 。这两者都相对善于处理长序列，但 RNN 无法并行化。我们可能会考虑结合它们以获得更好的总体表现，但一篇有名的文章12指出，其实只用 Self-Attention 就可以达到好得多的效果。具体的，其构建了一个被称作 Transformer Block 的结构，如下图所示：

    简单的说，对于输入数据，其首先经过带有 Residual Connection 的 Multi-heads Self-Attention Layer ，然后做 Layer Normalization ，然后经过带有 Residual Connection 的并行 FCNN ，最后做 Layer Normalization ，得到结果。

    在 Transformer 当中，实际上不同输入间交流的唯一方式就是 Self-Attention 。Transformer 的好处在于其是高度可并行的，适于实际计算。而在原论文中所搭建的 Transformer Model 由 12 个 Transformer Block 构成，前 6 个 block 作为 encoder ，后 6 个作为 decoder ，overall width 均为 512 ，number of heads 均为 6 。

    然后的事情我们就都知道了，Transformer 彻底击败了 RNN 成为了 NLP 中最主流的模型，就如同当年 AlexNet 在 Image Classification 中击败了所有非深度学习的模型一般。13

  1. 这个模型和先前描述的模型其实有些区别。首先我们多保存了一个 context ，这可能是为了方便引入下文的 attention 的；另一方面，我们将上一步的输出作为了下一步的输入。理论上这些信息都是由 hidden vector 产生的，可以认为 hidden vector 应该在一定程度上包含了这些信息。我猜测输入这些看似多余的信息是为了为模型提供某种提示，补全丢失的信息。↩︎

  2. 需要了解为什么 softmax 如此常用。↩︎

  3. 一个细节是 没有作为 的输入。不知道这里为什么排除了 ，可能是忘画了。↩︎

  4. 感觉像钻石剑。↩︎

  5. Xe at al, Show, Attend, and Tell: Neural Image Caption Generation with Visual Attentions, ICML 2015. 这篇文章中提供了一些有趣的可视化。↩︎

  6. Justin 还提到这样的做法可能受到了生物学上人眼观察物体的启发，但我觉得这些看法比较平凡，就不写了。↩︎

  7. 最先 似乎实现为全连接网络，但后来发现向量内积的效果其实也还好。↩︎

  8. 有些时候 Self-Attention Layer 也会加上 Residual Connection 。例如这篇文章 Zhang et al, Self-Attention Generative Adversarial Networks, ICML 2018.↩︎

  9. 还是考虑句子理解。显然之后的词语不应该影响之前的词语。↩︎

  10. 可能是相对于副对角线而言的。↩︎

  11. 没看出来这样搞有什么用。可能是为了省复杂度吧。多头这个名字听起来倒是很厉害。↩︎

  12. Vaswani et al, Attention is all you need, NeurIPS 2017.↩︎

  13. 但是看起来 Transformer 的计算复杂度还是显著高于 RNN 的，前者为 而后者仅为 。↩︎

  • 标题: 注意力机制
  • 作者: RPChe_
  • 创建于 : 2025-03-18 00:00:00
  • 更新于 : 2025-03-19 00:55:44
  • 链接: https://rpche-6626.github.io/2025/03/18/DL/ATT/
  • 版权声明: 本文章采用 CC BY-NC-SA 4.0 进行许可。
推荐阅读
循环神经网络 循环神经网络 如何训练神经网络 如何训练神经网络 卷积神经网络的可视化与可解释性 卷积神经网络的可视化与可解释性
推荐阅读
循环神经网络 循环神经网络 如何训练神经网络 如何训练神经网络
评论
目录
注意力机制
  1. 问题背景
  2. 算法描述
    1. Attention for RNN with Machine Translation
    2. Attention for CNN with Image Captioning
    3. Attention Layer
    4. Self-Attention Layer
  3. RNN, Self-Attention 与 Transformer