如何训练神经网络

RPChe_
  2025-03-11 2025-03-11 创建   2025-03-18 20:39:04 2025-03-18 20:39:04 更新    3.6k 字  12 分钟  

简要介绍了训练神经网络的技术细节，并引入了 Transfer Learning 这一思想。

训练前

  • 本节将会介绍激活函数的选择、对训练数据的处理、参量的初始化以及正则化的选择。

激活函数

  • 激活函数是一个非线性函数，其作用是改变网络层的输出，避免网络的表达能力减弱，以区别 Linear Classifier ；另一方面，激活函数也可以视作对神经元的所谓 firing rate 的模拟。

    激活函数的选择是多样的，一般有以下几种：

    我们对以上的几种激活函数做一个简要的评论。

    1. Sigmoid 。这是最早的选择之一。Sigmoid 有很多坏处，主要是：

      1. Sigmoid 在偏离 0 的位置会导致梯度消失，这使得模型迭代缓慢，很难收敛。
      2. Sigmoid 不是 0 centered 。更确切的说，Sigmoid 是恒正的。这同样会给模型的迭代造成问题。具体的，我们考虑 sigmoid 的下一层网络，不妨假设这是一个全连接层。考虑与某一个 hidden unit 有关的所有参数，由于经过了 Sigmoid ，它们的 local gradient 一定全是正的。而与这些参量有关的 upstream gradient 是一个标量，因此这些参量关于损失函数的 gradient 一定是同号的。假设一共有 个这样的参量，那么在优化空间 中我们只能向两个象限移动，而象限总数是 ，这很容易使得优化时要做阶梯状的蠕动，导致迭代缓慢。
      3. exp 算得很慢。

      其实最主要的问题是第一点，其余两点相比之下影响很小。对于第二点，实际上训练的时候我们是会取一个 mini batch ，然后计算它们的梯度的均值的，这实际上会有很大的改善。

    2. tanh 。这其实是对 Sigmoid 的改进。但是它还是会导致梯度消失。

    3. ReLU 。这其实是一个很现代的选择。它的最大优点是解决了梯度消失问题，从而使得模型的收敛速度比 Sigmoid 快了非常多。但 ReLU 仍然不是 0 centered ，而且在负数上没有梯度。这会导致另一个问题，称作 Dead ReLU ，即如果当前的参量远离数据点，使得所有输出全是负的，那梯度就永远不会传播了。1 但实践中其实人们一般不用担心这种问题，因为它很少出现。

    4. Leaky ReLU 。这是对 ReLU 的改进，主要目标是避免 dead ReLU 出现。这样做会引入一个超参数，我们也可以选择去学习它，这样就得到了 PReLU 。

    5. ELU 。还是对 ReLU 的改进，可以保证输出是 0 centered 。如果给 ELU 乘一个特定的系数 ，并且固定特定的 ，就得到了 SELU 。理论上 SELU 具备 Self-Normalizing 性质，即使不用 Batch Normalization 也可以训练深度网络，但是我们无意详谈。2

    总体来说，激活函数的选择其实没什么大的区别。Justin 建议用 ReLU 就行，还有别用 Sigmoid 和 tanh 。3

数据预处理

  • 一般来说，给定数据点，常见的预处理方式是减去其均值再归一化其方差，或者也可以做 PCA 和 Whitening 。这样搞的好处，我猜测是有助于改善精度问题。比方说考虑用通过原点的超平面划分数据，在减去均值之前，分类结果可能对参量的微小变动很敏感；而减去均值之后，数据点会离原点更近，从而对参量的微小变动不那么敏感。4
  • 图像预处理的方案有对每个像素点减去均值，或者对每个 channel 减去均值再归一化方差。

参量初始化

  • 现在考虑如何初始化神经网络中的参数矩阵。具体而言，理想的初始化应该可以保证通畅的梯度传播。一个不错的办法是直接给矩阵填入采样自高斯分布的小随机数，但是对于深层网络来说，这样会出问题。具体的，我们以全连接层为例，考虑计算其输出的方差，得到：

    假设激活函数是 tanh ，其在 0 附近表现为单位函数。如果 ，那么随着深度的推进，方差会趋于 0 ，每一层的输出也会趋 0 ，导致反向传播的梯度也趋 0 ；如果 ，那么方差会发散，输出会进入 tanh 的 saturated regime ，梯度又会趋 。所以我们希望 ，这样便使得方差保持定值。5

    然而如果使用 ReLU 作为激活函数，这样操作还是会导致方差趋于 0 。大致原因是 ReLU 每次都强制一半的输出变成 0 ，所以减小了方差。相应的解决方案则是令 。6

    如果我们考虑 Residual Block ，会发现以上的操作又失效了。这时的解决方案是，对于 Residual Block 的第一层，采用 MSRA Initialization ；而对于第二层，直接初始化为 0 。78

正则化

  • 正则化的目的是避免过拟合。之前我们已经介绍过了 初始化，其旨在让模型在优化损失函数之外再做点别的事，比如使得参数分布更均匀。下面我们会介绍一些别的 Regularization 。

Dropout

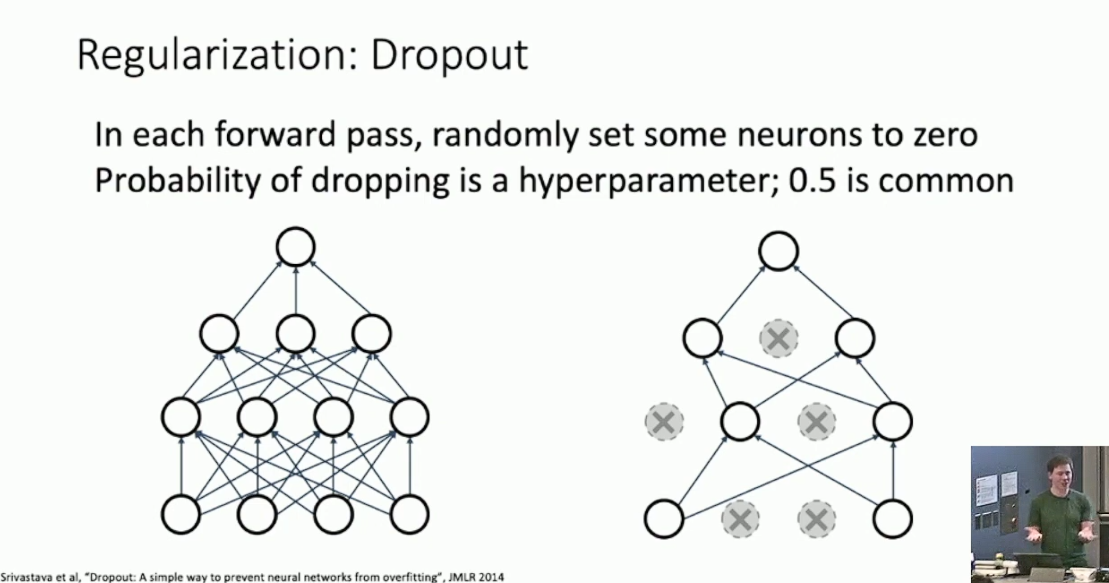
  • Dropout 主要用于全连接层。其思想是，每一次由当前层向后更新时，我们都以固定概率（例如 0.5）随机丢弃一些节点，如下图所示：

    除开引入随机性从而避免过拟合之外，这样做还有一个好处，就是使得模型在丢弃一部分节点后仍然可以分类。这样做有利于强制不同的节点辨认图片的某些特征，而非整体，从而提高了 Robustness 。9 而训练完成以后，为了去除随机性，我们希望对所有情况做平均，而这是很难办到的。一个折衷的方法是，我们考虑每一个神经元受上一层的贡献，发现就是全连接时的贡献再乘上不丢弃的概率，于是我们直接按照这个观察进行计算。10

    另一方面，我们也可以将 Dropout 看成某种集成学习，即我们同时训练了很多共享参数，但结构不同的模型，最后再做平均。

Normalization

  • Batch Normalization 也可以视作 Regularization。这是因为我们的计算结果和 mini batch 的取法是有关的，自然引入了随机性。
  • 特别的，Dropout 一般只用于全连接层，而后来的 CNN 基本很少用全连接层了。这时采取的 regularization 一般就是 Batch Normalization 。

Data Augmentation

  • 我们也可以考虑对训练集做随机变化来增强数据集，也就引入了随机性。常用的方式包括随机裁剪、改变尺寸，随机去掉图片的一部分（Cutout）、或者将不同的图片混在一块（Mixup）。

其它方式

  • Fractional Max Pooling（做随机大小的 pooling）、Stochastic Depth（随机跳过一些 Layer 或者 Block）、Drop Connect（随机去掉全连接层往后贡献的转移边），之类的，选择很多。推荐的方式包括 Batch Normalization 、Data Augmentation 、Cutout 和 Mixup 。

训练中

学习率的设置

  • 一般的选择是将学习率设置为常数，在很多时候这都是一个很好的选择。另外也可以考虑设置变化的学习率，比方说每过 30 个 epoch 就将学习率减小到原先的 0.1 ，称作 Step learning rate 。11 另一个常见的选择是 Cosine learning rate ，按照： 这是 CV 领域较为传统的选择。而 NLP 方向则一般会倾向于线性的学习率： 另外还有一些比较小众的选择，例如 Inverse root learning rate ：1213

如何看待学习曲线

  • 我们最关注的学习曲线一般是损失函数曲线（作散点图并求均值）以及训练集和验证集上的正确率。我们一般会考虑在损失函数不再有明显下降时减小学习率。而如果在训练集上正确率提升时验证正确率下降，说明产生过拟合，我们可能会考虑选择验证正确率最高处的参量，或者调整正则化、引入更多数据。如果两个正确率离得很近，说明模型还是欠拟合，我们可能会考虑急需训练，或者增大参数量。总体来说，两个正确率都应该增长，并带有一定差距。

如何选择超参数

  • 一般的选择是作 Grid Search ，即为每个超参数选择一些值 14，然后尝试所有组合，选出最好的一个。这样做的坏处是，假设我们做了 次尝试，那么单一超参数上的采样是 级别的。一个相对更好的方式是，我们为每个超参数选定一个区间，然后随机尝试 次，每个超参数均独立随机采样。这样就可以让单一超参数的采样增大到 级别。

  • 理论上我们也可以对超参数做优化，例如做 Gradient Descent 之类的，但是这样的计算开销太大了。这方面其实也有一些研究，但我们无意深入。

  • 最后我们将给出一个选择超参数的范式。15

    1. 关闭正则化，使用采样自小方差高斯分布的参量进行单次计算，查看输出是否符合预期，从而避免网路写挂。
    2. 关闭正则化，使用小训练集训练模型，并过拟合。其旨在通过快速调整找到较好的网络结构、学习率以及参量初始化的设置。
    3. 使用上一步的网络结构，打开正则化，使用所有训练数据，找到合适的学习率，使得前 100 步迭代内损失函数有显著下降。
    4. 在上一步的基础上找到大致的超参数区间，然后训练 1 到 5 个 epoch 。
    5. 调整参数区间，延长训练。
    6. 查看学习曲线。
    7. 回到第五步。

训练后

  • 我们可能会希望对训练后的模型做一些调整或整合，本节将简要介绍。

模型集成

  • 训练多个模型，然后将它们的概率分布取均值，或者使用投票法之类的。
  • 或者也可以截取模型训练过程中的快照来集成。为此，我们可能会考虑使用周期性的学习率，并在低点保存模型。
  • 或者取训练过程中的参量的指数均值之类的。16

迁移学习

  • 迁移学习是一个相当重要的思想，即将大数据集上已有的模型迁移到小数据集上。一个典型的例子是，使用 ImageNet 上训练完成的模型，例如 VGG 16 ，去除最后的全连接层，迁移到 Caltech101 上，并冻结所有参数，就可以取得比单独训练的模型好得多的成果。17 而这样的现象是相当广泛的。18

    一般的，我们可以考虑将大数据集上训练完成的模型的参数冻结、去除最后的全连接层，用作图像特征提取器。然后我们再使用 SVM 来划分不同的类别。这样的方式一般适用于与大数据集具备较高相似度的小数据集 19，例如 ImageNet 与 Caltech101 。

    另一个方式则被称作 Fine-Tuning ，即，我们去除训练完成的模型的最后的全连接层，然后添加适用于新数据集的全连接层。具体的，我们可以考虑先用 feature extractor 训练一个 Linear Classifier ，然后将其连接到模型上形成最后的全连接层，再做整体的训练。特别的，使用 Fine-Tuning 时一般需要减小学习率，有时我们也会考虑冻结模型的浅层参数以节省计算资源。Fine-Tuning 一般要求新数据集不能太小，同时冻结的层数也是与数据集的相似度有关的。

分布式训练

  • 先别管这个。哥们也没几张卡。

  1. 可能的解决方案是，给输出加上一个小正数。↩︎

  2. 参见 Klambauer et al, Self-Normalizing Neural Network, ICLR 2017 上的 91 页证明。↩︎

  3. 特别的，激活函数一般都是单调的。一个看法是非单调函数可能会导致信息的损失，这是我们所不希望的。↩︎

  4. 没看出来有什么别的道理，所以不详谈了。↩︎

  5. 称为 Xavier Initialization 。↩︎

  6. 称为 MSRA Initialization 。可以想象我们通过这种方式抵消了 ReLU 导致的方差缩减。↩︎

  7. 阻断了层之间的方差传递，直接令 Residual Path 传递相同的方差。↩︎

  8. 如何初始化参数矩阵这个问题其实有很多研究，Justin 列出了其中的一部分。↩︎

  9. Justin 的 slides 里还有一些很直观的图例。为了控制篇幅，这里没有放。↩︎

  10. 这样做是无法计算真实的平均值的，但是实践中的表现已经足够好了。↩︎

  11. ResNet 的训练就用到了这样的技巧。epoch 指固定次数的迭代，比方说 300 次。↩︎

  12. 被用于 Vaswanl et al, Attention is all you need, NeurIPS 2017 。↩︎

  13. 一般来说，我们希望变动量与参数大小（ 范数之类的）的比值在 0.001 左右。↩︎

  14. 一般是 linear 的。↩︎

  15. 特别的，我们可以使用 Cross Validation 来并行训练模型。数据可视化则推荐 Tensor Board 。↩︎

  16. 类似于 x_test = 0.995 * x_test + 0.005 * x 。其中 x 是参量。称作 Polyak Averaging 。↩︎

  17. 当然，一般在 ImageNet 上表现更好的模型迁移以后也会更好。需要指出的是，迁移是一个好的选择，但不一定是必要的。在新数据集上单独训练可能也能取得不错的成果，但是一般而言耗时会更长。另一方面，预训练非常耗时，相比之下扩大数据集可能是更有效的选择。↩︎

  18. 可以广泛的迁移到其它模型、其它问题当中。↩︎

  19. 如果相似度不高，可以考虑把中间层的结果拿来当特征向量跑 Linear Classifier 试试。↩︎

  • 标题: 如何训练神经网络
  • 作者: RPChe_
  • 创建于 : 2025-03-11 00:00:00
  • 更新于 : 2025-03-18 20:39:04
  • 链接: https://rpche-6626.github.io/2025/03/11/DL/train/
  • 版权声明: 本文章采用 CC BY-NC-SA 4.0 进行许可。
推荐阅读
卷积神经网络 卷积神经网络 神经网络 神经网络 卷积神经网络的可视化与可解释性 卷积神经网络的可视化与可解释性
推荐阅读
卷积神经网络 卷积神经网络 神经网络 神经网络
评论
目录
如何训练神经网络
  1. 训练前
    1. 激活函数
    2. 数据预处理
    3. 参量初始化
    4. 正则化
      1. Dropout
      2. Normalization
      3. Data Augmentation
      4. 其它方式
  2. 训练中
    1. 学习率的设置
    2. 如何看待学习曲线
    3. 如何选择超参数
  3. 训练后
    1. 模型集成
    2. 迁移学习
    3. 分布式训练