即 Neural Networks 。

问题背景

算法描述

很多时候数据集都不是线性可分的。老的解决方案是，考虑将数据点通过某种方式映射到特征空间中去，使得特征空间中的数据点变得容易划分，例如 SVM 的 Kernel Trick 。特征提取方式是多样的，例如 Color Histogram 、Histogram of Oriented Gradients 或者 Bag of Words 。但一个更加 SOTA 的方式则是神经网络。
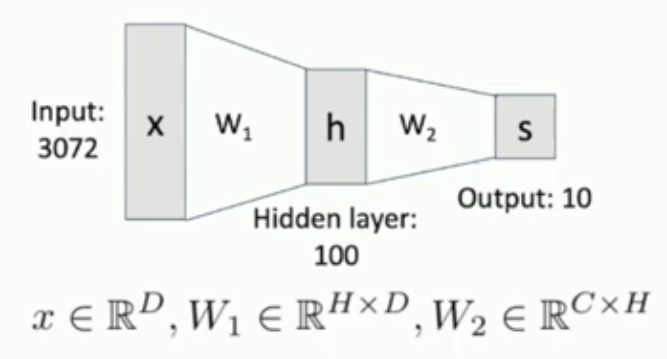
具体的，我们将从 Linear Classifer 改进得到 Neural Network 。考虑最简单的 Linear Classifer 的预测方式：¹ 现在我们考虑加入另一个矩阵，得到：我们将这个模型称作一个两层的神经网络。如图所示：

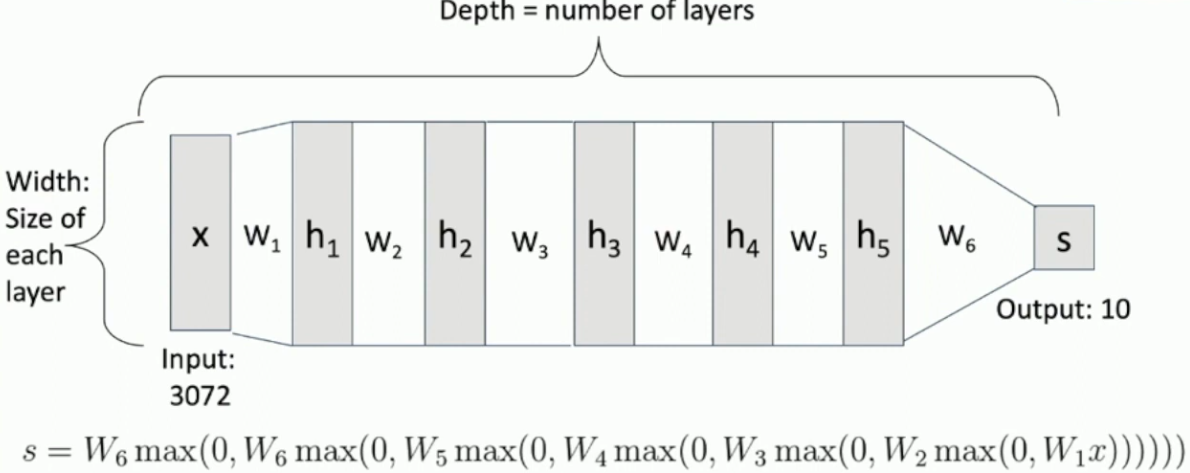
我们将这个函数称作神经网络的激活函数，更具体的，称作 ReLU（Rectified Linear Unit）。激活函数对于神经网络而言是相当重要的，因为，去掉激活函数以后，多层神经网络的表达能力实际上和一般的 Linear Classifier 没有本质区别。²激活函数有很多不同的种类，ReLU 是最为常见的一种。

我们将每一层的点称作神经元（Neuron），并将这样的神经网络称作全连接神经网络（Fully Connected Neural Network），这是因为输入层的每一个神经元都参与决定了下一层的所有神经元的值。下图展示了一个六层的神经网络，每一层的 hidden units（即中间层的神经元个数）都是相等的（一般都会这样安排），我们将 hidden units 的个数称作神经网络的宽度（width）：³

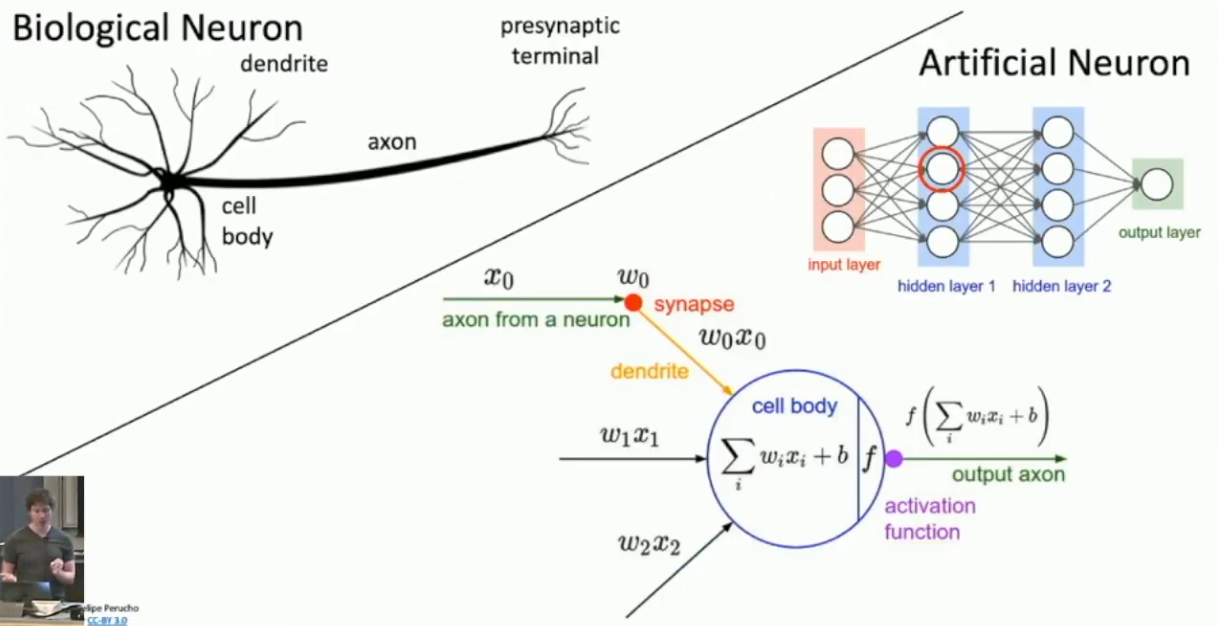
实际上，Neural Nerwork 和生物学神经网络并没有必然的联系，相对准确的说法是前者的发明受到了后者的启发。在这里我们就大致讲讲两者之间的相似性。
我们可以想象，生物学神经网络是由大量神经元通过某种方式相互连接而形成的，其中每一个神经元通过轴突接受电信号，再通过树突发射电信号。我们假设发射出的电信号可以被表示为接受的电信号的线性组合再复合某个非线性函数（激活函数）的值，这样我们就可以仿照建立 Neural Network 。

当然，我们建立的 Neural Network 相对于生物学神经网络是非常简化的。

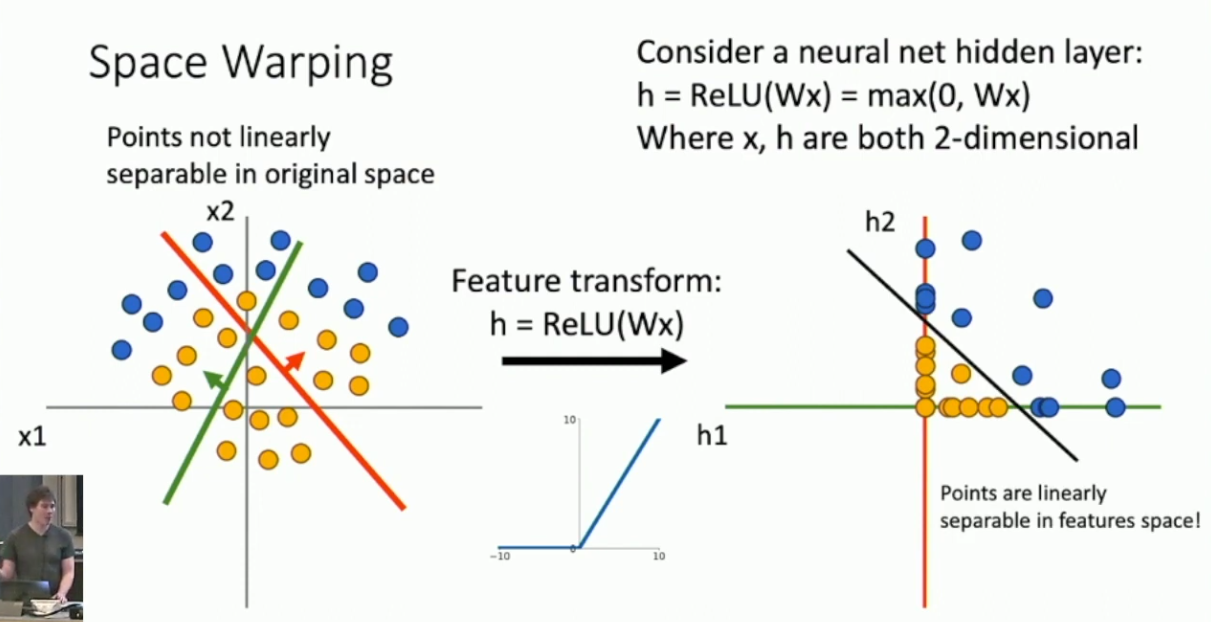
我们期待多层神经网络的表达能力要强于一般的 Linear Classifier 。不妨考虑神经网络的几何意义。先考虑单层神经网络，其实际上仍然是用了若干个超平面来划分类别。这几个超平面应该应该把整个空间划分为了若干块，然后通过 ReLU 函数，我们把所有点都集中到了其中的一块上。最后，我们在这一块空间上进行下一层神经网络的划分。因此，可以看出，由于激活函数的作用，深层神经网络的超平面对应到浅层的空间就不再是线性的了。浅层神经网络通过线性划分而扭曲了空间，从而增强了深层网络的表达能力。

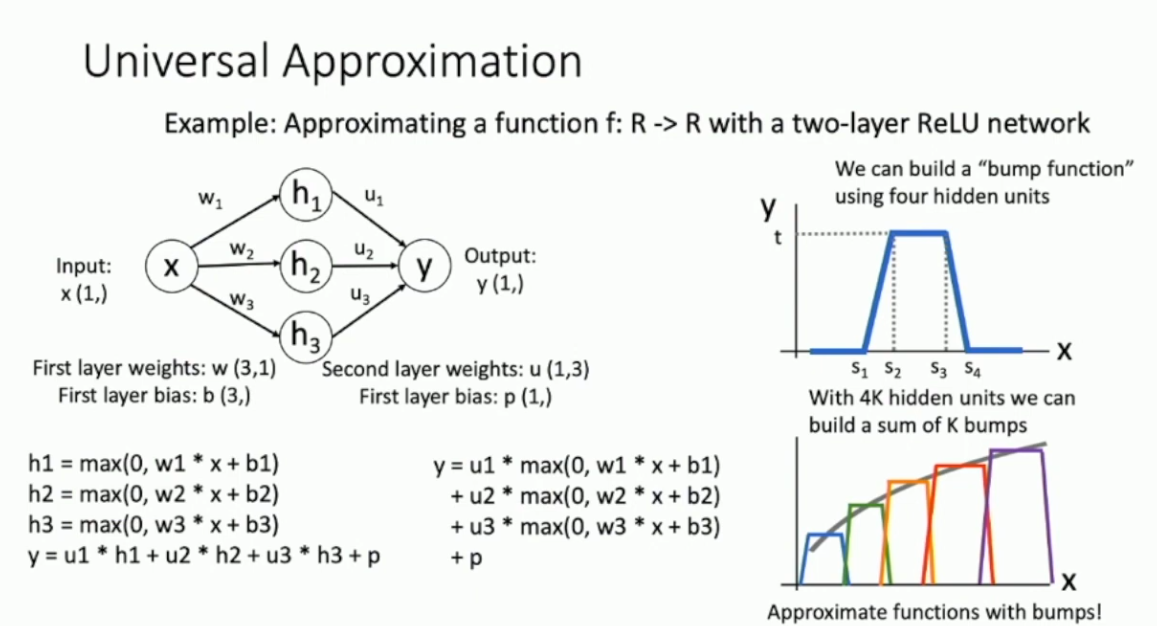
严格地说，我们可以将图像分类问题视作函数拟合问题。即，我们希望通过某种方式来拟合一个函数，而后者则表示了所有图像的分类结果。我们可以证明，不低于两层的神经网络是具备 Universal Approximation 性质的。证明的思路其实比较简单，就是通过 ReLU 函数来构造基本单元，再用基本单元来做任意精度的拟合。以为例，Proof Sketch 如下图所示：

特别的，这里的神经网络是带有 bias term 的。