即 Back Propagation 。如果你试着实现过神经网络，你就会发现进行梯度下降时手工计算神经网络的损失函数的形式导数是极为繁琐的。所以现在我们要来谈点求导的技术。

问题背景

给定一个相对复杂的神经网络及其损失函数，求解其单点处的数值导数。

算法描述

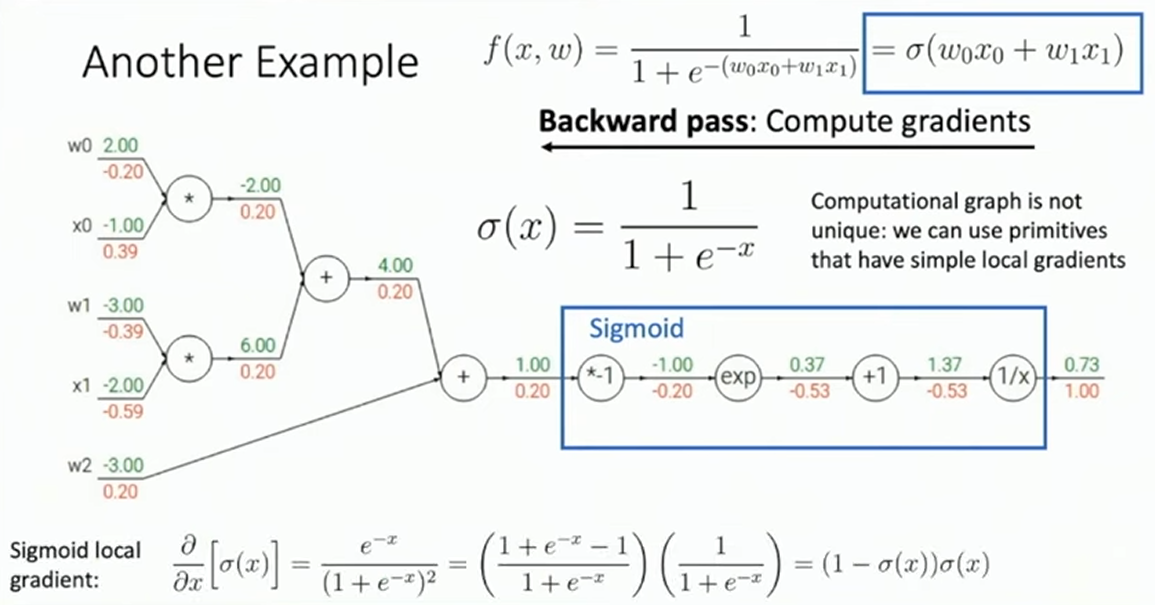
现在我们要先引入一个概念，即 Computational Graph 。考虑以下函数：其 Computational Graph 为：

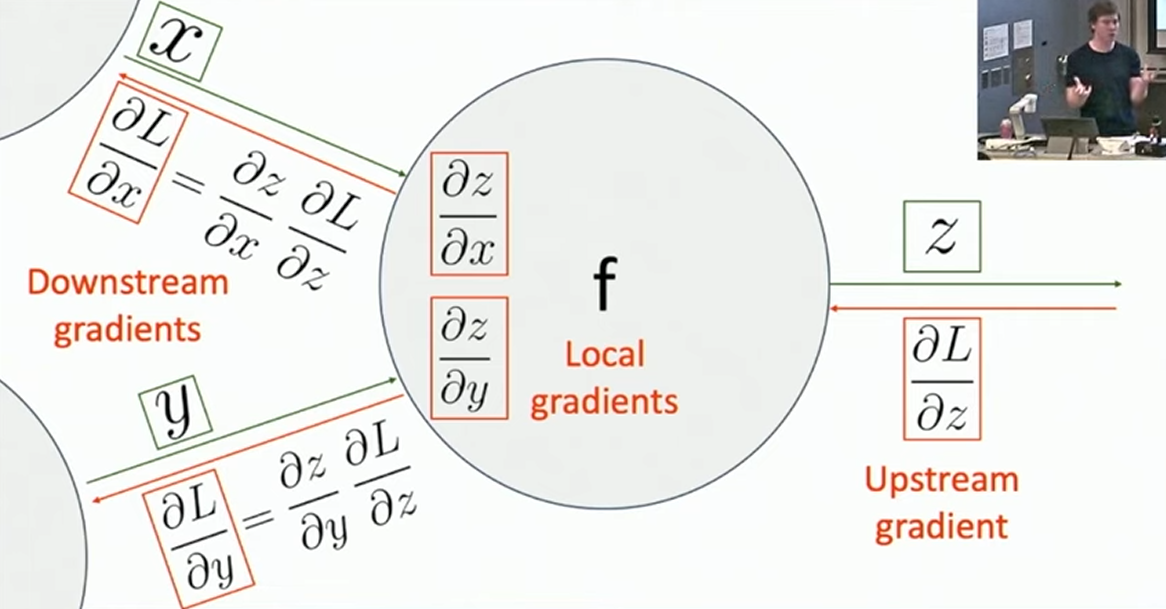
可以看出，Computational Graph 的结构与表达式树类似，它们都以图的方式刻画了表达式的运算过程，每一个入度为的节点都对应了一个运算数，而其余的节点对应了某种运算。不同之处在于 Computational Graph 是一张 DAG（有向无环图），即每一个节点可以向多个后继节点贡献。容易看出，表达式的运算在 Computational Graph 上是按照拓扑序进行的。我们将这一按照拓扑序进行运算得到结果的过程称作 Forward Pass 。现在我们再考虑如何从 Computational Graph 上得到所有参数的偏导数。我们将代表运算符的节点视作中间变量，假设我们已经求得了中间变量的偏导数（称作 upstream gradient），并希望推知的前驱节点与的偏导数（称作 downstream gradient），如下图所示：

可以看出，通过求导的链式法则，我们只需求关于的偏导数（称作 local gradient），就可以推出 downstream gradient 。那么，我们只需从 Computational Graph 唯一的根节点出发，逆拓扑序进行递推，就可以简单的推出损失函数关于图上所有节点的偏导数。¹这样做的好处是：
1. 省去了繁琐的计算。因为现在我们只用关心局部的形式导数了。
2. 效率极高。通过一来一去两次遍历 Computational Graph 我们就可以求得所有参数的偏导数。
3. 模块化，利于封装。如果我们想要调整神经网络，现在我们只需替换 Computational Graph 中对应的节点。特别的，我们不一定要把表达式拆成最基本的运算单元，而只需保证每个运算节点都便于求导且模块化。
可以看出最重要的求偏导的过程是逆拓扑序进行的，所以我们将上述算法称作反向传播。

反向传播的实现

首先，反向传播不仅对求解复杂网络的数值导数有用，其对于求解简单网络的形式导数也极有帮助。实际上，基于 Computational Graph 的反向传播的观点，我们只需将求解的过程倒过来就可以得到求导的框架了。
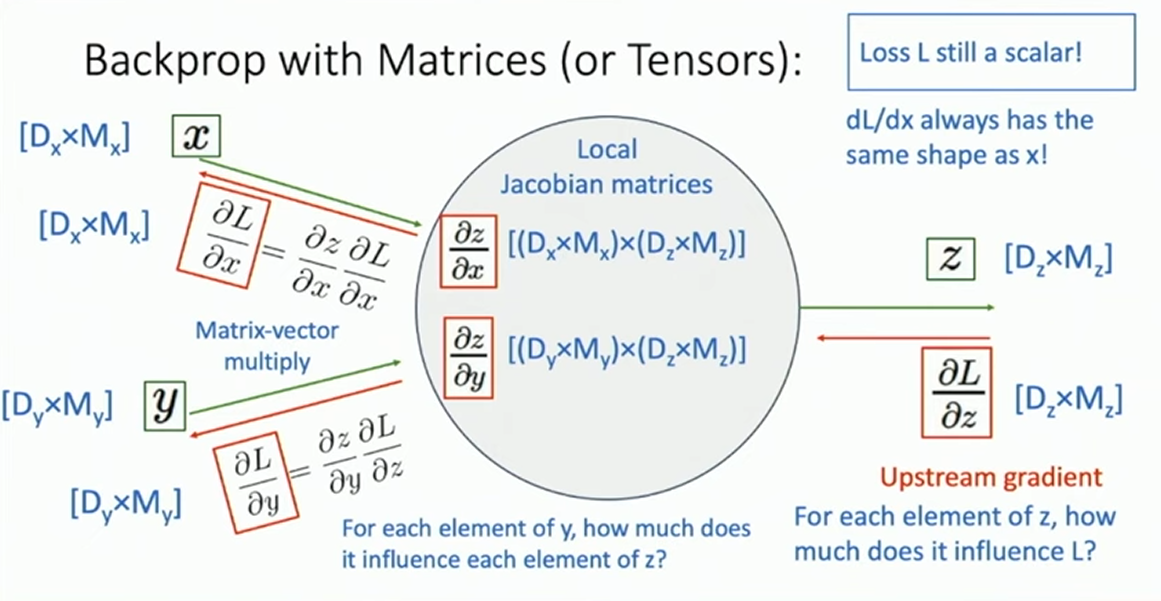
特别的，有时 Computation Graph 上的计算会涉及到张量²。这时一个相对好的处理方式是，跟踪后继中的单一变量的梯度，最后将其整合为一体，统一计算。而一个比较取巧的思路是，反正我们知道 updtream 、downstream 和 local 的所有张量的形状，所以我们只需要想办法把这些形状凑出来（例如通过矩阵乘法），再检验即可。

其余的机器求导方式

Back Propagation 也被称作 backward mode automatic differentiation 。这是因为，我们可以将以上的逆推求导的过程看作计算所有局部的导数，再用链式法则把它们乘起来得到答案。显然导数的乘法是有结合律的，所以我们也可以正着做这件事情，这就是 forward mode automatic differentiation 。但是我并不知道这样做有什么好处，所以就不详谈了。
Back Propation 也可用于求任意的高阶导数，只需将高阶微分看作连续的一阶微分，再对应的构造 Computational Graph 即可。这一部分我没有细看，就也不详谈了。

对于出度不为一的节点，将其后继的导数加起来作为 upstream gradient 即可。↩︎
仅涉及到向量及标量的运算相对易于处理。这里的张量沿用了 pytorch 中的概念，其实就是高维数组。↩︎