关于红黑树

鉴于我所可以找到的关于这个数据结构的资料都不够理想，我在这里做一个简要的总结。

红黑树的性质

• 红黑树是一种自平衡的二叉搜索树，特点是每个节点额外存储了一个“颜色”信息，可以为红或黑。

• 我们对红黑树的结构提出一些要求。具体的，我们希望¹：

  1. 根节点为黑。
  2. 红结点的儿子必为黑。
  3. 叶子结点为虚拟点，且颜色必为黑²。
  4. 任何叶子结点到根的路径上的黑结点个数相同，称作黑高度。

  对于包含 个数据的红黑树，其一共有 个结点。记黑高度为 ，则显然红黑树中包含了一棵深度为 的满二叉树，于是我们有： 而红黑树的高度不超过 ，因此红黑树的高度同为 。

红黑树的插入操作

• 为了不影响黑高度，我们将数据作为红节点按照 BST 的一般方式插入。接下来，考虑：

  1. 若插入点恰为根节点，则将颜色修正为黑，结束。

  2. 若插入后不存在双红，直接结束。

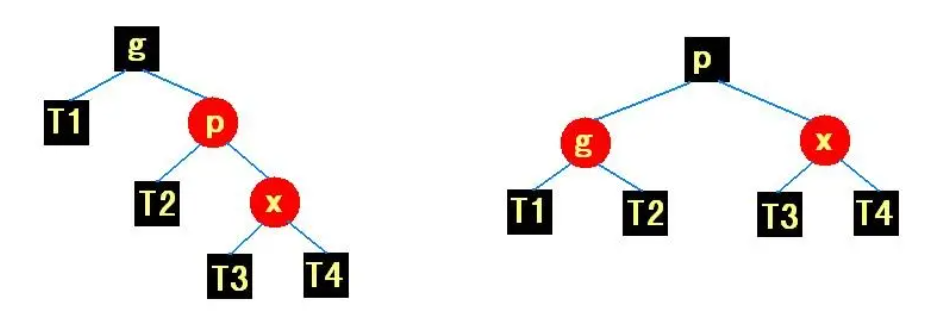
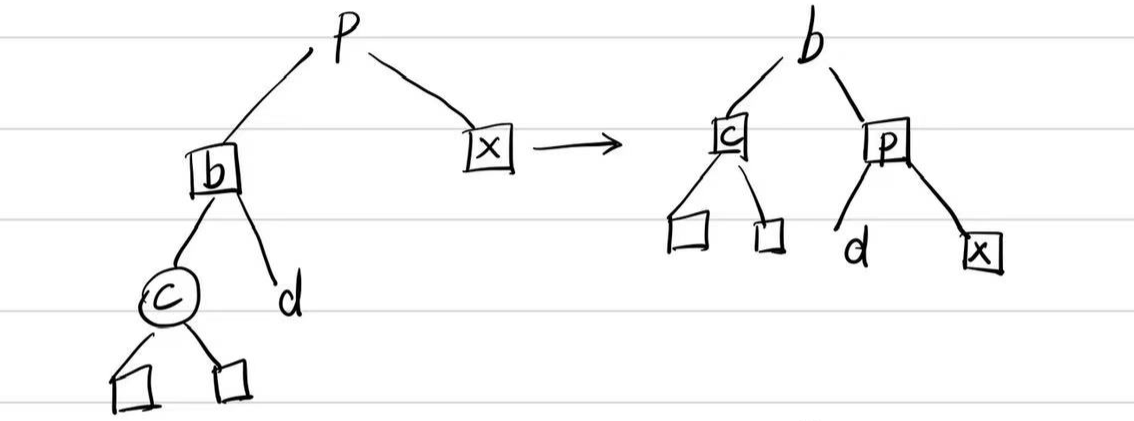
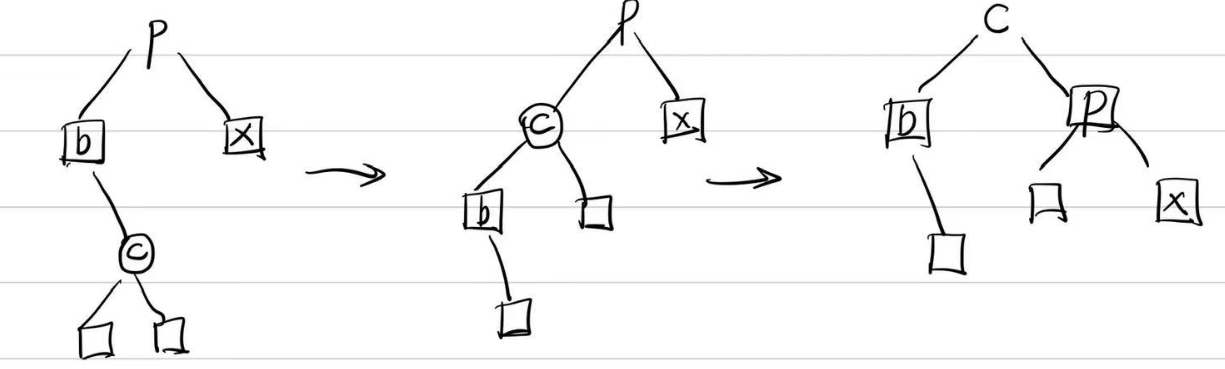
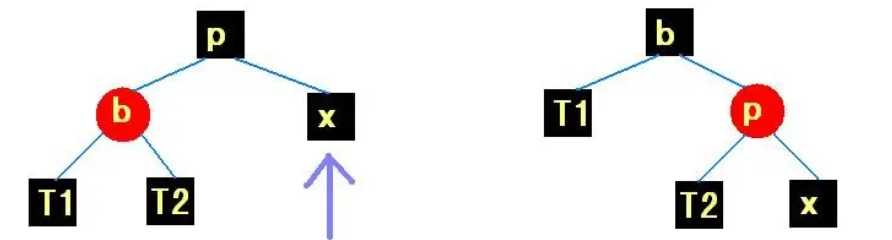
  3. 若插入点父亲的兄弟为黑，按照下图修正，然后结束：

     

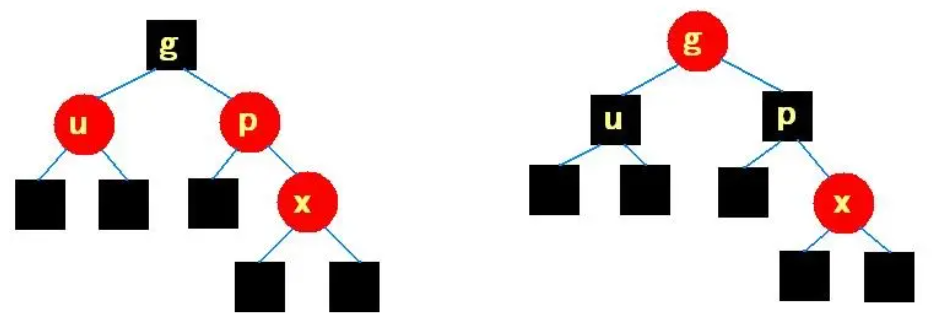
  4. 若插入点父亲的兄弟为红，按照下图修正，并对插入点的祖父递归：

     

红黑树的删除操作

• 先按照 BST 的一般方式删除目标数据。即先定位待删除结点，再考虑：

  1. 若其仅有一个非虚拟儿子，则此儿子必为红，该节点必为黑。使用儿子替代该节点，并染黑即可。
  2. 若其有两个非虚拟儿子，则定位该节点的后继，以后继的数据替代该节点，并删除后继。
  3. 若其无虚拟儿子，则直接删除。

  以上，在情况 3 中，若该结点颜色为黑，则删除过程破坏了红黑树的性质四，即删除位置对应的叶子结点的黑高度比其余叶子小一。此时需要执行修正操作，以保持性质四。具体的，假定当前结点颜色为黑，且子树内所有叶子的黑高度相等，比其余叶子小一，考虑：

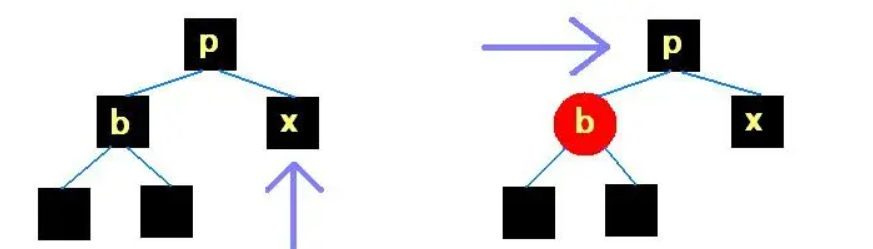
  1. 兄弟为黑且无红儿子，父亲为黑。按照下图调整，并向父亲递归：

     

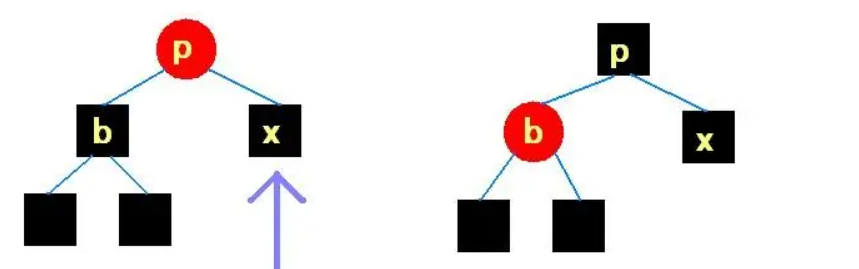
  2. 兄弟为黑且无红儿子，父亲为红。按照下图调整，并结束：

     

  3. 兄弟为黑且同向儿子为红。按下图调整，并结束：

     

  4. 兄弟为黑且异向儿子为红。按下图调整，并结束：

     

  5. 兄弟为红。按下图调整，并转情况 2 到 4 。

     

---

1. 不同的资料中对红黑树的要求可能存在些微不同。↩︎

2. 以下，请读者根据语境判断是否考虑虚拟结点。↩︎